题目内容
圆x2+y2-4x-4y-10=0上的点到直线x+y-14=0的最大距离与最小距离的差是( )
| A.36 | B.18 | C. | D.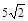 |
C
分析:先看直线与圆的位置关系,如果相切或相离最大距离与最小距离的差是直径;
相交时,圆心到直线的距离加上半径为所求.
解答:解:圆x2+y2-4x-4y-10=0的圆心为(2,2),半径为3 ,
,
圆心到到直线x+y-14=0的距离为 =2
=2 >3
>3 ,
,
圆上的点到直线的最大距离与最小距离的差是2R=6 ,
,
故选C.
相交时,圆心到直线的距离加上半径为所求.
解答:解:圆x2+y2-4x-4y-10=0的圆心为(2,2),半径为3
 ,
,圆心到到直线x+y-14=0的距离为
 =2
=2 >3
>3 ,
,圆上的点到直线的最大距离与最小距离的差是2R=6
 ,
,故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 外一点
外一点 作圆
作圆 ,
,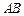 与
与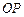 交于点
交于点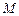 ,设
,设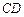 为过点
为过点 四点共圆.
四点共圆.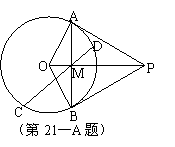
 ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为 .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响. 率;
率; 弃所有的考试机会,记他参加考试的次数为
弃所有的考试机会,记他参加考试的次数为 ,求
,求 上一点
上一点 引圆
引圆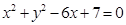 的切线,则切线长的最小值为
的切线,则切线长的最小值为



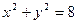 内有一点
内有一点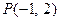 ,
,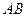 为过点
为过点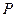 的直线。
的直线。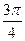 时,求弦
时,求弦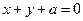 与圆
与圆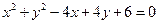 有交点,则实数
有交点,则实数 的取值范围是( )
的取值范围是( )




 AB于D点,则CD= 。
AB于D点,则CD= 。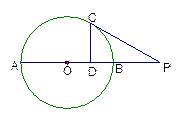
 表示圆心在第四象限的圆,则实数
表示圆心在第四象限的圆,则实数 的范围为 .
的范围为 .