题目内容
2.若sin(270°+θ)=2cos(90°+θ),则cos2θ+sinθcosθ-sin2θ的值为1.分析 由诱导公式可将已知条件化为cosθ=2sinθ,再结合cos2θ+sin2θ=1即可解出cos2θ,sin2θ,sinθcosθ,从而得出答案.
解答 解:∵sin(270°+θ)=2cos(90°+θ),
∴-cosθ=-2sinθ,即cosθ=2sinθ,
∵cos2θ+sin2θ=1,
∴cos2θ=$\frac{4}{5}$,
sin2θ=$\frac{1}{5}$,
sinθcosθ=2sin2θ=$\frac{2}{5}$.
∴cos2θ+sinθcosθ-sin2θ=$\frac{4}{5}$+$\frac{2}{5}$-$\frac{1}{5}$=1.
故答案为:1.
点评 本题考查了三角函数的诱导公式及同角三角函数的关系,是基础题.

练习册系列答案
相关题目
12.已知集合A={x|x2-4x-5<0},B={x|2<x<4},则A∩B=( )
| A. | (1,3) | B. | (1,4) | C. | (2,3) | D. | (2,4) |
10.已知椭圆x2+$\frac{{y}^{2}}{9}$=1的上、下两个焦点分别为F,F′.G是椭圆上任意一点,已知椭圆的上顶点为A.下顶点为A′.左顶点为B.右顶点为B′.若点M为AB的中点.则|GM|+|GF′|的最大值( )
| A. | 6+$\sqrt{3}$ | B. | 6-$\sqrt{3}$ | C. | 6+$\frac{\sqrt{42-24\sqrt{2}}}{2}$ | D. | 6-$\frac{\sqrt{42-24\sqrt{2}}}{2}$ |
17.若cos65°=a,则sin25°的值是( )
| A. | -a | B. | a | C. | $\sqrt{1-{a}^{2}}$ | D. | -$\sqrt{1-{a}^{2}}$ |
12.若函数$f(x)=-\frac{1}{2}{({x-2})^2}+alnx$在(1,+∞)上是减函数,则实数a的取值范围是( )
| A. | .[-1,+∞) | B. | (-∞,-1] | C. | (1,+∞) | D. | .(-∞,1] |
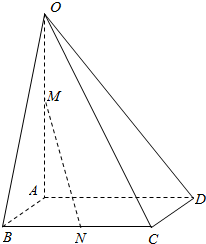 如图,在四棱锥O-ABCD中,底面ABCD为平行四边形,M为OA的中点,N为BC的中点,求证:MN∥平面OCD.
如图,在四棱锥O-ABCD中,底面ABCD为平行四边形,M为OA的中点,N为BC的中点,求证:MN∥平面OCD.