题目内容
13.已知函数f(x)=x2+2x|x-a|,其中a∈R.(1)当a=-1,求函数f(x)的单调区间;
(2)若不等式f(x)≥3在x∈[1,3]上恒成立,求a的取值范围.
分析 (1)f(x)=$\left\{\begin{array}{l}{-(x+1)^{2},x≤-1}\\{3(x+\frac{1}{3})^{2}-\frac{1}{3},x>-1}\end{array}\right.$,利用二次函数的单调性即可得出;
(2)f(x)=$\left\{\begin{array}{l}{-(x-a)^{2}+{a}^{2},x≤a}\\{3(x-\frac{a}{3})^{2}-\frac{{a}^{2}}{3},x>a}\end{array}\right.$,通过对a分类讨论,利用二次函数的单调性即可得出.
解答 解:(1)f(x)=$\left\{\begin{array}{l}{-(x+1)^{2},x≤-1}\\{3(x+\frac{1}{3})^{2}-\frac{1}{3},x>-1}\end{array}\right.$,
f(x)在(-∞,-1)和$(-\frac{1}{3},+∞)$上递增,在在$(-1,-\frac{1}{3})$上递减.
(2)f(x)=$\left\{\begin{array}{l}{-(x-a)^{2}+{a}^{2},x≤a}\\{3(x-\frac{a}{3})^{2}-\frac{{a}^{2}}{3},x>a}\end{array}\right.$,
当a≥0时,f(x)在(-∞,a)和(a,+∞)上均递增,∵f(a)=a2,则f(x)在R上递增;
当a<0时,f(x)在(-∞,a)和$(\frac{a}{3},+∞)$上递增,在在$(a,\frac{a}{3})$上递减;
可知,f(x)在x∈[1,2]上恒递增,
则fmin(x)=f(1)=1+2|1-a|≥3,解得a≤0或a≥2.
点评 本题考查了二次函数的单调性、分类讨论方法,考查了数形结合思想方法、推理能力与计算能力,属于中档题.

 口算题天天练系列答案
口算题天天练系列答案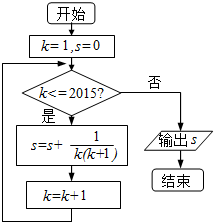 执行如图所示的程序框图,输出的s为( )
执行如图所示的程序框图,输出的s为( )| A. | $\frac{2015}{2016}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2016}{2015}$ | D. | $\frac{2017}{2016}$ |
| A. | (1,3) | B. | ( 1,6) | C. | (2,4) | D. | (2,6) |