题目内容
14．
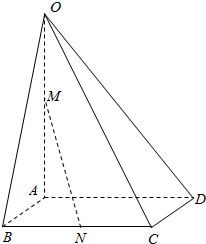如图，在四棱锥O-ABCD中，底面ABCD为平行四边形，M为OA的中点，N为BC的中点，求证：MN∥平面OCD．
分析 欲证MN∥平面OCD，根据直线与平面平行的判定定理可知只需证MN与平面OCD内一直线平行，取OD的中点E，连接CE，ME，根据平行四边形可知MN∥CE，而MN?平面OCD，CE?平面OCD，满足定理所需条件．
解答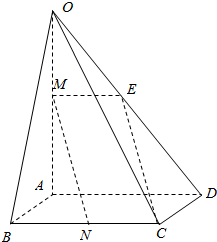 
证明：取OD的中点E，连接CE，ME，
因为ME∥NC，ME=NC，
所以MENC为平行四边形，则MN∥CE，
而MN?平面OCD，CE?平面OCD，
∴MN∥平面OCD．
点评 本题主要考查了直线与平面平行的判定，判断或证明线面平行的常用方法有：①利用线面平行的定义（无公共点）；②利用线面平行的判定定理（a?α，b?α，a∥b⇒a∥α）；③利用面面平行的性质定理（α∥β，a?α⇒a∥β）；④利用面面平行的性质（α∥β，a?α，a?，a∥α⇒?a∥β）．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
19．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-bx+c\\;x≥0}\\{{e}^{x}\\;x＜0}\end{array}\right.$，其中b=$\frac{2}{π}$${∫}_{-2}^{2}$$\sqrt{4-{x}^{2}}$dx，c为目标函数z=2x+4y在约束条件$\left\{\begin{array}{l}{y≥0}\\{x+y-1≤0}\\{x-y+2≥0}\end{array}\right.$，内的最大值，则f（x）＜10的解集为（ ）
| A． | （-∞，0） | B． | [0，5） | C． | （-∞，5） | D． | （-∞，5] |
4．
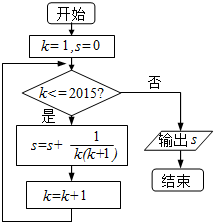执行如图所示的程序框图，输出的s为（ ）
执行如图所示的程序框图，输出的s为（ ）| A． | $\frac{2015}{2016}$ | B． | $\frac{2014}{2015}$ | C． | $\frac{2016}{2015}$ | D． | $\frac{2017}{2016}$ |