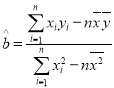题目内容
【题目】椭圆
的离心率是
，且以两焦点间的线段为直径的圆的内接正方形面积是
.
（1）求椭圆
的方程；
（2）过左焦点
的直线
与相交于
、
两点，直线
，过作垂直于的直线与直线
交于点
，求
的最小值和此时的直线的方程.
【答案】（1）
；（2）
的最小值为
，此时直线
的方程为
.
【解析】
（1）由离心率及圆内接正方形的面积和
、
、
之间的关系可求出椭圆的方程；
（2）由（1）可得左焦点
的坐标，设直线的方程与椭圆联立，求出两根之和及两根之积，进而求出弦长
的值，再由题意设
的方程，令
求出
的纵坐标，即求出了的坐标，进而求出
的值，求出所以比值的表达式，由均值不等式求出最小值.
（1）由题意可得
，解得
，
，
所以椭圆的方程为；
（2）由（1）得左焦点
，显然直线的斜率不为
，
设直线的方程为
，设
、
，
联立直线与椭圆的方程
，整理可得
，
，
，
所以弦长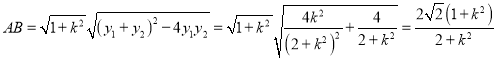
.
由题意设直线的方程为
，令可得
，即
，
所以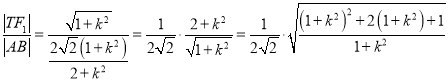
，
当且仅当
，即
时取等号，
所以的最小值为，此时直线的方程为.
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
相关题目
【题目】下表是某公司
年
月份研发费用
（百万元）和产品销量
（万台）的具体数据：
月 份 |
|
|
|
|
|
|
|
|
研发费用（百万元） |
|
|
|
|
|
|
|
|
产品销量（万台） |
|
|
|
|
|
|
|
|
（1）根据数据可知与之间存在线性相关关系，用线性相关系数说明与之间的相关性强弱程度
（2）求出与的线性回归方程（系数精确到
），并估计当研发费用为
（百万元）时该产品的销量.
参考数据：
，
，
，
参照公式：相关系数
，其回归直线
中的
