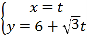题目内容
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 和
和![]() 两点.
两点.
(1)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
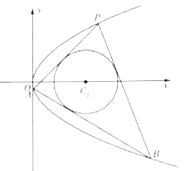
(2)若过点![]() 且垂直于直线
且垂直于直线![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,记
两点,记![]() 与
与![]() 的面积分别为
的面积分别为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)12.
;(2)12.
【解析】
(1) 设直线方程为![]() ,联立直线与抛物线的方程,利用韦达定理求解得
,联立直线与抛物线的方程,利用韦达定理求解得![]() 即可.
即可.
(2) 联立直线与抛物线的方程,利用韦达定理表达![]() ,再根据基本不等式的方法求最小值即可.
,再根据基本不等式的方法求最小值即可.
解: (1)由直线![]() 过定点
过定点![]() ,可设直线方程为
,可设直线方程为![]() .
.
联立![]() 消去
消去![]() ,得
,得![]() ,
,
由韦达定理得![]() ,
,
所以![]() .
.
因为![]() .所以
.所以![]() ,解得
,解得![]() .
.
所以直线![]() 的方程为
的方程为![]() .
.
(2)由(1),知![]() 的面积为
的面积为![]()
![]() .
.
因为直线![]() 与直线
与直线![]() 垂直,
垂直,
且当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,则此时直线
,则此时直线![]() 的方程为
的方程为![]() ,
,
但此时直线![]() 与抛物线
与抛物线![]() 没有两个交点,
没有两个交点,
所以不符合题意,所以![]() .因此,直线
.因此,直线![]() 的方程为
的方程为![]() .
.
同理,![]() 的面积
的面积![]() .
.
所以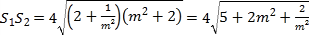
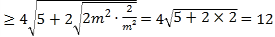 ,
,
当且仅当![]() ,即
,即![]() ,亦即
,亦即![]() 时等号成立.
时等号成立.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】下表是某公司2018年5~12月份研发费用(百万元)和产品销量(万台)的具体数据:
月 份 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
研发费用(百万元) | 2 | 3 | 6 | 10 | 21 | 13 | 15 | 18 |
产品销量(万台) | 1 | 1 | 2 | 2.5 | 6 | 3.5 | 3.5 | 4.5 |
(Ⅰ)根据数据可知![]() 与
与![]() 之间存在线性相关关系,求出
之间存在线性相关关系,求出![]() 与
与![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(Ⅱ)该公司制定了如下奖励制度:以![]() (单位:万台)表示日销售,当
(单位:万台)表示日销售,当![]()
![]() 时,每位员工每日奖励200元;当
时,每位员工每日奖励200元;当![]() 时,每位员工每日奖励300元;当
时,每位员工每日奖励300元;当![]() 时,每位员工每日奖励400元.现已知该公司某月份日销售
时,每位员工每日奖励400元.现已知该公司某月份日销售![]() (万台)服从正态分布
(万台)服从正态分布![]() (其中
(其中![]() 是2018年5-12月产品销售平均数的二十分之一),请你估计每位员工该月(按30天计算)获得奖励金额总数大约多少元.
是2018年5-12月产品销售平均数的二十分之一),请你估计每位员工该月(按30天计算)获得奖励金额总数大约多少元.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数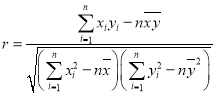 ,其回归直线
,其回归直线![]() 中的
中的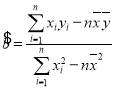 ,若随机变量
,若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() .
.
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸.呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院![]() 人进行了问卷调查得到了如下的列联表:
人进行了问卷调查得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 |
| ||
女 |
| ||
合计 |
|
已知在全部![]() 人中随机抽取
人中随机抽取![]() 人,抽到患心肺疾病的人的概率为
人,抽到患心肺疾病的人的概率为![]() .
.
(1)请将上面的列联表补充完整,并判断是否有![]() 的把握认为患心肺疾病与性别有关?请说明你的理由;
的把握认为患心肺疾病与性别有关?请说明你的理由;
(2)已知在不患心肺疾病的![]() 位男性中,有
位男性中,有![]() 位从事的是户外作业的工作.为了指导市民尽可能地减少因雾霾天气对身体的伤害,现从不患心肺疾病的
位从事的是户外作业的工作.为了指导市民尽可能地减少因雾霾天气对身体的伤害,现从不患心肺疾病的![]() 位男性中,选出
位男性中,选出![]() 人进行问卷调查,求所选的
人进行问卷调查,求所选的![]() 人中至少有一位从事的是户外作业的概率.
人中至少有一位从事的是户外作业的概率.
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 ,其中
,其中![]() )
)