题目内容
【题目】在四棱锥P﹣ABCD中,△PAB是边长为2的等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,BC=CD=1,PD![]() .
.
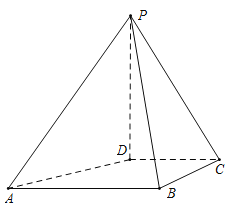
(1)证明:AB⊥PD.
(2)求二面角A﹣PB﹣C的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)根据勾股定理的逆定理、线面垂直的判定定理、线面垂直的性质进行证明即可;
(2)由AD2+BD2=AB2,可得AD⊥BD,以D为原点,DA为x轴,DB为y轴,DP为z轴,建立空间直角坐标系,根据空间向量夹角公式进行求解即可.
(1)证明:连结BD,
∵在四棱锥P﹣ABCD中,△PAB是边长为2的等边三角形,
底面ABCD为直角梯形,AB∥CD,AB⊥BC,BC=CD=1,PD![]() .
.
∴BD=AD![]() ,
,
∴AD2+PD2=AP2,BD2+PD2=PB2,
∴AD⊥PD,BD⊥PD,
∵AD∩BD=D,∴PD⊥平面ABCD,
∵AB平面ABCD,∴AB⊥PD.
(2)解:∵AD2+BD2=AB2,∴AD⊥BD,
以D为原点,DA为x轴,DB为y轴,DP为z轴,建立空间直角坐标系,
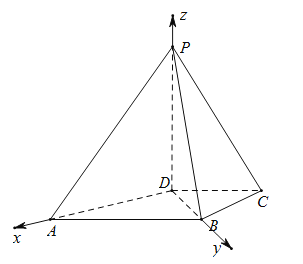
则A(![]() ,0,0),B(0,
,0,0),B(0,![]() ,0),C(
,0),C(![]() ,0),P(0,0,
,0),P(0,0,![]() ),
),
![]() (
(![]() ),
),![]() (0,
(0,![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() ,
,![]() ),
),
设平面ABP的法向量![]() (x,y,z),
(x,y,z),
则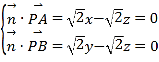 ,取x=1,得
,取x=1,得![]() (1,1,1),
(1,1,1),
设平面PBC的法向量![]() ,
,
则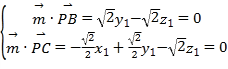 ,取
,取![]() ,得
,得![]() (﹣1,1,1),
(﹣1,1,1),
设二面角A﹣PB﹣C的平面角为θ,
则二面角A﹣PB﹣C的余弦值为:cosθ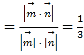 .
.

【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸.呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院![]() 人进行了问卷调查得到了如下的列联表:
人进行了问卷调查得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 |
| ||
女 |
| ||
合计 |
|
已知在全部![]() 人中随机抽取
人中随机抽取![]() 人,抽到患心肺疾病的人的概率为
人,抽到患心肺疾病的人的概率为![]() .
.
(1)请将上面的列联表补充完整,并判断是否有![]() 的把握认为患心肺疾病与性别有关?请说明你的理由;
的把握认为患心肺疾病与性别有关?请说明你的理由;
(2)已知在不患心肺疾病的![]() 位男性中,有
位男性中,有![]() 位从事的是户外作业的工作.为了指导市民尽可能地减少因雾霾天气对身体的伤害,现从不患心肺疾病的
位从事的是户外作业的工作.为了指导市民尽可能地减少因雾霾天气对身体的伤害,现从不患心肺疾病的![]() 位男性中,选出
位男性中,选出![]() 人进行问卷调查,求所选的
人进行问卷调查,求所选的![]() 人中至少有一位从事的是户外作业的概率.
人中至少有一位从事的是户外作业的概率.
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 ,其中
,其中![]() )
)
【题目】在综合素质评价的某个维度的测评中,依据评分细则,学生之间相互打分,最终将所有的数据合成一个分数,满分100分,按照大于或等于80分的为优秀,小于80分的为合格,为了解学生的在该维度的测评结果,在毕业班中随机抽出一个班的数据.该班共有60名学生,得到如下的列联表:
优秀 | 合格 | 总计 | |
男生 | 6 | ||
女生 | 18 | ||
合计 | 60 |
已知在该班随机抽取1人测评结果为优秀的概率为![]() .
.
(1)完成上面的列联表;
(2)能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系?
(3)现在如果想了解全校学生在该维度的表现情况,采取简单随机抽样方式在全校学生中抽取少数一部分来分析,请你选择一个合适的抽样方法,并解释理由.
附: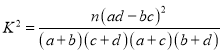
| 0.25 | 0.10 | 0.025 |
| 1.323 | 2.706 | 5.024 |