题目内容
【题目】在平面直角坐标系xOy中,A、B两点的坐标分别为(0,1)、(0,﹣1),动点P满足直线AP与直线BP的斜率之积为![]() ,直线AP、BP与直线y=﹣2分别交于点M、N.
,直线AP、BP与直线y=﹣2分别交于点M、N.
(1)求动点P的轨迹方程;
(2)求线段MN的最小值;
(3)以MN为直径的圆是否经过某定点?若经过定点,求出定点的坐标;若不经过定点,请说明理由.
【答案】(1)![]() (x≠0).(2)4
(x≠0).(2)4![]() .(3)是,定点(0,﹣2+2
.(3)是,定点(0,﹣2+2![]() )或(0,﹣2﹣2
)或(0,﹣2﹣2![]() ).
).
【解析】
(1)设动点![]() ,再根据斜率之积化简方程即可.
,再根据斜率之积化简方程即可.
(2)分别设![]() 关于的
关于的![]() 的方程,再联立
的方程,再联立![]() 求解
求解![]() 的坐标,进而求得
的坐标,进而求得![]() 关于
关于![]() 的解析式,再利用
的解析式,再利用![]() 化简,利用基本不等式求解最小值即可.
化简,利用基本不等式求解最小值即可.
(3)根据题意可知![]() ,再进行根据
,再进行根据![]() 满足椭圆的方程代入化简求解即可.
满足椭圆的方程代入化简求解即可.
(1)设动点P(x,y),∵A(0,1),B(0,﹣1),
∴直线AP的斜率k1![]() ,直线BP的斜率
,直线BP的斜率![]() ,
,
又k1k2![]() ,∴
,∴![]() ,
,
∴动点P的轨迹方程为![]() (x≠0).
(x≠0).
(2)设直线AP的方程为y﹣1=k1(x﹣0),
直线BP的方程为y+1=k2(x﹣0),
由![]() ,得
,得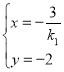 ,∴M(
,∴M(![]() ),
),
由![]() ,得
,得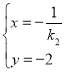 ,∴N(
,∴N(![]() ,﹣2),
,﹣2),
由![]() ,得|MN|=|
,得|MN|=|![]() |=|
|=|![]() |
|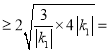 4
4![]() ,
,
当且仅当![]() ,即
,即![]() 时,等号成立,
时,等号成立,
∴线段MN长的最小值为4![]() .
.
(3)设点Q(x,y)是以MN为直径的圆的任意一点,则![]() ,
,
即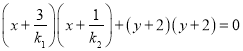 ,
,
又k1k2![]() ,
,
∴以MN为直径的圆的方程为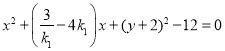 ,
,
令x=0,得(y+2)2=12,解得y=﹣2![]() ,
,
∴以MN为直径的圆过定点(0,﹣2+2![]() )或(0,﹣2﹣2
)或(0,﹣2﹣2![]() ).
).

 金博士一点全通系列答案
金博士一点全通系列答案【题目】某面包店推出一款新面包,每个面包的成本价为4元,售价为10元,该款面包当天只出一炉(一炉至少15个,至多30个),当天如果没有售完,剩余的面包以每个2元的价格处理掉.为了确定这一炉面包的个数,该店记录了这款新面包最近30天的日需求量(单位:个),整理得下表:
日需求量 | 15 | 18 | 21 | 24 | 27 |
频数 | 10 | 8 | 7 | 3 | 2 |
(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)以30天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为24,记当日这款新面包获得的总利润为![]() (单位:元).
(单位:元).
(i)若日需求量为15个,求![]() ;
;
(ii)求![]() 的分布列及其数学期望.
的分布列及其数学期望.