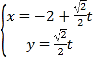��Ŀ����
����Ŀ��ij������Ƴ�һ���������ÿ������ijɱ���Ϊ4Ԫ���ۼ�Ϊ10Ԫ���ÿ��������ֻ��һ¯��һ¯����15��������30�������������û�����꣬ʣ��������ÿ��2Ԫ�ļ۸�����.Ϊ��ȷ����һ¯����ĸ������õ��¼�������������30���������������λ���������������±���
�������� | 15 | 18 | 21 | 24 | 27 |
Ƶ�� | 10 | 8 | 7 | 3 | 2 |
��1�����ݱ������ݿ�֪��Ƶ��![]() ����������
����������![]() ����λ������������أ���
����λ������������أ���![]() ����
����![]() �����Իع鷽�̣�
�����Իع鷽�̣�
��2����30���¼�ĸ�����������Ƶ�ʴ�������������ĸ��ʣ����õ�����������¯�ĸ���Ϊ24���ǵ�������������õ�������Ϊ![]() ����λ��Ԫ��.
����λ��Ԫ��.
��i������������Ϊ15������![]() ��
��
��ii����![]() �ķֲ��м�����ѧ����.
�ķֲ��м�����ѧ����.
���𰸡���1��![]() ��2����i��72 ��ii���ֲ��м�������
��2����i��72 ��ii���ֲ��м�������![]() Ԫ.
Ԫ.
��������
��1�����![]() ��
��![]() ��
��![]() ��
��![]() ���ɴ������
���ɴ������![]() ����
����![]() �����Իع鷽��.
�����Իع鷽��.
��2����i������������Ϊ15���������![]() Ԫ.
Ԫ.
��ii������������Ϊ18������![]() Ԫ������������Ϊ21������
Ԫ������������Ϊ21������![]() Ԫ������������Ϊ24����27������
Ԫ������������Ϊ24����27������![]() Ԫ���ɴ������
Ԫ���ɴ������![]() �ķֲ��к�
�ķֲ��к�![]() .
.
�⣺��1��![]() ��
��
![]() ��
��
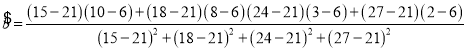
![]() ��
��
![]() ��
��
��![]() ����
����![]() �����Իع鷽��Ϊ
�����Իع鷽��Ϊ![]() .
.
��2����i������������Ϊ15������![]() Ԫ.
Ԫ.
��ii������������Ϊ18������![]() Ԫ��
Ԫ��
����������Ϊ21������![]() Ԫ��
Ԫ��
����������Ϊ24����27������![]() Ԫ��
Ԫ��
��![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| 72 | 96 | 120 | 144 |
|
|
|
|
|
![]() Ԫ.
Ԫ.

����Ŀ�����л�������·��ͨ��ȫ������47������ع涨���������о����к��ʱ��Ӧ���������У�����������ͨ�����к����Ӧ��ͣ�����У��׳ơ����ð����ߡ������л�������·��ͨ��ȫ���� ��90���涨���Բ��������˵ļ�ʻԱ���Կ�3�֣�����50Ԫ�Ĵ���.�±���ij��һ����·�ڼ���豸��ץ�ĵ�5�����ڼ�ʻԱ�������ð����ߡ���Ϊͳ�����ݣ�
�·� | 1 | 2 | 3 | 4 | 5 |
Υ�¼�ʻԱ���� | 120 | 105 | 100 | 90 | 85 |
��1������������������Υ������y���·�֮��Ļع�ֱ�߷���![]() +
+![]()
��2��Ԥ���·��7�·ݵIJ������ð����ߡ�Υ�¼�ʻԱ������
��3����������5������ͨ����·�ڵļ�ʻԱ����������50�ˣ������ʻԱ�������ð����ߡ���Ϊ�����Ĺ�ϵ���õ�����2![]() ��������
��������
�����ð����� | ���ð����� | �ϼ� | |
���䲻����1�� | 22 | 8 | 30 |
����1������ | 8 | 12 | 20 |
�ϼ� | 30 | 20 | 50 |
�ܷ�ݴ��ж���97.5![]() �İ�����Ϊ�����ð����ߡ���Ϊ������йأ�
�İ�����Ϊ�����ð����ߡ���Ϊ������йأ�
�ο���ʽ�����ݣ� ,
,![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ������n=a+b+c+d��
������n=a+b+c+d��