题目内容
若函数y=f(x)满足:集合A={f(n)|n∈N*}中至少有三个不同的数成等差数列,则称函数f(x)是“等差源函数”,则下列四个函数中,“等差源函数”的个数是( )
①y=2x+1;
②y=log2x;
③y=2x+1;
④y=sin(
x+
)
①y=2x+1;
②y=log2x;
③y=2x+1;
④y=sin(
| π |
| 4 |
| π |
| 4 |
| A、1 | B、2 | C、3 | D、4 |
考点:进行简单的合情推理
专题:综合题,推理和证明
分析:利用新定义,进行验证即可得出结论.
解答:解:①y=2x+1,n∈N*,是等差源函数;
②∵log21,log22,log24构成等差数列,∴y=log2x是等差源函数;
③y=2x+1不是等差源函数,因为若是,则2(2p+1)=(2m+1)+(2n+1),则2p+1=2m+2n,
∴2p+1-n=2m-n+1,左边是偶数,右边是奇数,故y=2x+1不是等差源函数;
④y=sin(
x+
)是周期函数,显然是等差源函数.
故选:C.
②∵log21,log22,log24构成等差数列,∴y=log2x是等差源函数;
③y=2x+1不是等差源函数,因为若是,则2(2p+1)=(2m+1)+(2n+1),则2p+1=2m+2n,
∴2p+1-n=2m-n+1,左边是偶数,右边是奇数,故y=2x+1不是等差源函数;
④y=sin(
| π |
| 4 |
| π |
| 4 |
故选:C.
点评:本题考查等差源函数的判断与证明,是中档题,解题时要认真审题,注意反证法的合理运用.

练习册系列答案
相关题目
设平面α与平面β相交于直线l,直线a?α,直线b?β,b∥l,则“a∥β”是“a∥b”的( )
| A、充分而不必要条件 | B、必要而不充分条件 | C、充要条件 | D、既不充分又不必要条件 |
已知函数f(x)=(x+a)2-7lnx+1在(1,+∞)上单调递增,则实数a的取值范围为( )
A、(
| ||
B、[
| ||
C、(-∞,
| ||
D、(-∞,-
|
调查某医院某段时间内婴儿出生的时间与性别的关系,得到下面的数据表:
你认为婴儿的性别与出生时间有关系的把握为( )
| 晚上 | 白天 | 合计 | |
| 男婴 | 24 | 30 | 54 |
| 女婴 | 8 | 26 | 34 |
| 合计 | 32 | 56 | 88 |
| A、80% | B、90% |
| C、95% | D、99% |
已知复数z满足(3+4i)z=25,则z=( )
| A、3-4i | B、3+4i | C、-3-4i | D、-3+4i |
设i是虚数单位,复数i3+
=( )
| 2i |
| 1+i |
| A、-i | B、i | C、-1 | D、1 |
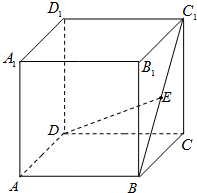 如图,在正方体ABCD-A1B1C1D1中,E为BC1的中点,则DE与面BCC1B1所成角的正切值为( )
如图,在正方体ABCD-A1B1C1D1中,E为BC1的中点,则DE与面BCC1B1所成角的正切值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
矩阵A=
,向量
=
,则A10
=( )
|
| α |
|
| α |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|