题目内容
随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下列联表:性别与读营养说明列联表
(1)根据以上列联表进行独立性检验,能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系?
(2)从被询问的16名不读营养说明的大学生中,随机抽取2名学生,求抽到男生人数ξ的分布列及其均值(即数学期望).
(注:K2=
,其中n=a+b+c+d为样本容量.)
| 男 | 女 | 总计 | |
| 读营养说明 | 16 | 8 | 24 |
| 不读营养说明 | 4 | 12 | 16 |
| 总计 | 20 | 20 | 40 |
(2)从被询问的16名不读营养说明的大学生中,随机抽取2名学生,求抽到男生人数ξ的分布列及其均值(即数学期望).
(注:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
考点:独立性检验的应用,离散型随机变量的期望与方差
专题:
分析:(1)根据性别与看营养说明列联表,求出K2的观测值k的值,再根据P(K2≥6.635)=0.01,判断大学生“性别与在购买食物时看营养说明”有关;
(2)根据题意看出变量的可能取值,结合变量对应的事件和等可能事件的概率公式,写出变量的概率.列出分布列和期望值.
(2)根据题意看出变量的可能取值,结合变量对应的事件和等可能事件的概率公式,写出变量的概率.列出分布列和期望值.
解答:解:(1)假设H0:大学生性别与在购买食物时看营养说明无关,则K2应该很小.
根据题中的列联表得k2=
≈6.666>6.635,
由P(K2≥6.635)=0.01,
有99%的把握认为大学生“性别与在购买食物时看营养说明”有关.
故在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系;
(2)ξ的取值为0,1,2,则
P(ξ=0)=
=
;P(ξ=1)=
=
;P(ξ=2)=
=
,
∴ξ的分布列为:
∴ξ的期望为:Eξ=0×
+1×
+2×
=
.
根据题中的列联表得k2=
| 40×(16×12-4×8)2 |
| 20×20×16×24 |
由P(K2≥6.635)=0.01,
有99%的把握认为大学生“性别与在购买食物时看营养说明”有关.
故在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系;
(2)ξ的取值为0,1,2,则
P(ξ=0)=
| ||
|
| 11 |
| 20 |
| ||||
|
| 2 |
| 5 |
| ||
|
| 1 |
| 20 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 11 |
| 20 |
| 2 |
| 5 |
| 1 |
| 20 |
| 1 |
| 2 |
点评:本题主要考察读图表、独立性检验以及离散型随机变量的数学期望等基础知识,考查运用概率统计知识解决简单实际问题的能力,数据处理能力和应用意识.

练习册系列答案
相关题目
不等式x+
≥2成立的一个必要不充分条件是( )
| 1 |
| x |
| A、(0,+∞) |
| B、(0,1) |
| C、(-1,+∞) |
| D、(1,+∞) |
已知f(x)=3x2+5,则从0.1到0.2的平均变化率为( )
| A、0.3 | B、0.6 | C、0.9 | D、1.2 |
已知回归直线的斜率的估计值是1.2,样本点的中心为(4,5),则回归直线方程是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若复数z1=1+2i,z2=1-i,其中i是虚数单位,则(z1+z2)i在复平面内对应的点在( )
| A、第一象限 | B、第二象限 | C、第三象限 | D、第四象限 |

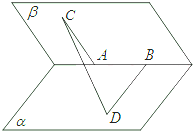 如图,60°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=2,AC=3,BD=4,求CD的长.
如图,60°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=2,AC=3,BD=4,求CD的长.