题目内容
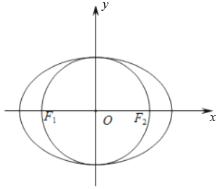
【题目】在平面直角坐标系xOy中,椭圆![]() 左、右焦点分别为
左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,两准线间距离为8,圆O的直径为
,两准线间距离为8,圆O的直径为![]() ,直线l与圆O相切于第四象限点T,与y轴交于M点,与椭圆C交于点N(N点在T点上方),且
,直线l与圆O相切于第四象限点T,与y轴交于M点,与椭圆C交于点N(N点在T点上方),且![]() .
.
(1)求椭圆C的标准方程;
(2)求直线l的方程;
(3)求直线l上满足到![]() ,
,![]() 距离之和为
距离之和为![]() 的所有点的坐标.
的所有点的坐标.
【答案】(1)![]() (2)
(2)![]() .(3)
.(3)![]() 和
和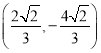 .
.
【解析】
(1) 根据椭圆的性质、离心率和两准线间的距离,列出以下方程:![]() ①,
①,![]() ②,
②,![]() ③,然后求解即可.
③,然后求解即可.
(2) 法一:设切点![]() ,则
,则![]() ⑤, 利用
⑤, 利用![]() 和
和![]() 为核心参数,依次表示直线OT的斜率,直线
为核心参数,依次表示直线OT的斜率,直线![]() 的方程,以及N点的坐标,然后列方程求解即可求出
的方程,以及N点的坐标,然后列方程求解即可求出![]() 和
和![]() ,进而即可求解.
,进而即可求解.
法二:设![]() ,
,![]() ,然后,以
,然后,以![]() ,
,![]() ,
,![]() 为核心参数,列出直线
为核心参数,列出直线![]() 的方程,又因
的方程,又因![]() 与
与![]() 相切,则列出圆心距
相切,则列出圆心距![]() 的方程,最后根据(1)中的方程,联合求解即可.
的方程,最后根据(1)中的方程,联合求解即可.
(3) 因为到![]() ,
,![]() 距离之和为
距离之和为![]() 的所有点的集合为椭圆C,
的所有点的集合为椭圆C,
所以满足题意的点为直线l与椭圆C的公共点,
联立![]() ④和
④和![]() ⑨得:
⑨得: ,然后求解即可.
,然后求解即可.
解:(1)设椭圆C的焦距为![]() ,因为离心率为
,因为离心率为![]() ①,
①,
两准线间距离为![]() ②,又
②,又![]() ③,
③,
由①②③解得![]() ,
,![]() .则椭圆C的标准方程为
.则椭圆C的标准方程为![]() ④
④
(2)法一:设切点![]() ,则
,则![]() ⑤,因T在第四象限,所以
⑤,因T在第四象限,所以![]() ,
,![]() ,
,
直线OT的斜率![]() ,因为
,因为![]() ,所以直线
,所以直线![]() 的斜率
的斜率![]() ,
,
直线![]() ,由⑤得:
,由⑤得:![]() ⑥,
⑥,
令![]() ,得
,得 ,
,
因为![]() ,
,![]() ,所以,T为MN中点,所以
,所以,T为MN中点,所以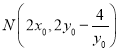 ,
,
代入(1)中④得: ,解得:
,解得:![]() ,
,![]() ,
,
代入⑥式得:直线l的方程为![]() .
.
法二:设![]() ,
,![]() ,则
,则![]() ⑤,设直线
⑤,设直线![]() ⑦,
⑦,
因为切点T在第四象限,所以![]() ,
,![]() ,
,![]() .
.
因l与![]() 相切,则圆心距
相切,则圆心距![]() ,
,![]() ⑧,
⑧,
因为![]() ,则
,则![]() ,所以
,所以![]() ⑨,
⑨,
联立⑤⑨解得:![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,
则![]() ,由⑧得
,由⑧得 ,解得
,解得![]() ,
,![]() .
.
当![]() 时,
时,![]() ,与
,与![]() 矛盾.则
矛盾.则![]() ,代入⑧,得
,代入⑧,得![]() ,
,
所以直线l方程为![]() ⑨.
⑨.
(3)因为到![]() ,
,![]() 距离之和为
距离之和为![]() 的所有点的集合为椭圆C,
的所有点的集合为椭圆C,
所以满足题意的点为直线l与椭圆C的公共点,
联立④⑨得: ,得
,得![]() ,即
,即 或
或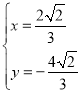 ,
,
所以满足条件的点的坐标为![]() 和
和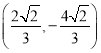 .
.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目