Question

【题目】已知函数.

（1）若函数在定义域上的最大值为1，求实数的值；

（2）设函数，当时，对任意的恒成立，求满足条件的实数的最小整数值.

Answer 1

【答案】（1）（2）.

【解析】

（1）先对函数求导，得到，分别讨论，两种情况，判定函数单调性，根据函数的最大值，即可求出结果；

（2）先由题意，将问题转化为：得到，对任意的恒成立；

再由，转化为：只需对任意的恒成立即可，令，用导数的方法求其最大值，即可得出结果.

（1）由题意，函数的定义域为，

当时，，在区间上单调递增，

∴在定义域上无最大值．

当时，令，，

由，得，，，

的单调递增区间为，的单调递减区间为，

所以函数，

即为所求．

（2）由，因为对任意的恒成立，

即，当时，对任意的恒成立，

∵，．

∴，

只需对任意的恒成立即可．

构造函数，，

∵，∴，且单调递增，

∵，，∴一定存在唯一的，使得

即，．∴单调递增区间为，单调递减区间为．

∴，

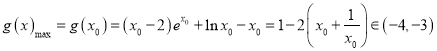∴的最小整数值为．