题目内容
【题目】某居民小区有两个相互独立的安全防范系统(简称系统)A和B,系统A和B在任意时刻发生故障的概率分别为 ![]() 和p.
和p.
(1)若在任意时刻至少有一个系统不发生故障的概率为 ![]() ,求p的值;
,求p的值;
(2)设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ,求ξ的概率分布列及数学期望Eξ.
【答案】
(1)解:设“至少有一个系统不发生故障”为事件C,则 ![]()
∴ ![]() ;
;
(2)解:ξ的可能取值为0,1,2,3
P(ξ=0)= ![]() ;P(ξ=1)=
;P(ξ=1)= ![]() ;
;
P(ξ=2)= ![]() =
= ![]() ;P(ξ=3)=
;P(ξ=3)= ![]() ;
;
∴ξ的分布列为
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
数学期望Eξ=0× ![]() +1×
+1× ![]() +2×
+2× ![]() +3×
+3× ![]() =
= ![]()
【解析】(1)求出“至少有一个系统不发生故障”的对立事件的概率,利用至少有一个系统不发生故障的概率为 ![]() ,可求p的值;(2)ξ的所有可能取值为0,1,2,3,求出相应的概率,可得ξ的分布列与数学期望.
,可求p的值;(2)ξ的所有可能取值为0,1,2,3,求出相应的概率,可得ξ的分布列与数学期望.
【考点精析】本题主要考查了离散型随机变量及其分布列的相关知识点,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.

【题目】![]() 市积极倡导学生参与绿色环保活动,其中代号为“环保卫士-
市积极倡导学生参与绿色环保活动,其中代号为“环保卫士-![]() ”的绿色环保活动小组对
”的绿色环保活动小组对![]() 年
年![]() 月-
月-![]() 年
年![]() 月(一月)内空气质量指数
月(一月)内空气质量指数![]() 进行监测,如表是在这一年随机抽取的
进行监测,如表是在这一年随机抽取的![]() 天的统计结果:
天的统计结果:
指数 |
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻微污染 | 轻微污染 | 中度污染 | 中重度污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(Ⅰ)若![]() 市某企业每天由空气污染造成的经济损失
市某企业每天由空气污染造成的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() (记为
(记为![]() )的关系为:
)的关系为: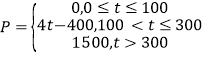 ,,在这一年内随机抽取一天,估计该天经济损失
,,在这一年内随机抽取一天,估计该天经济损失![]() 元的概率;
元的概率;
(Ⅱ)若本次抽取的样本数据有![]() 天是在供暖季节,其中有
天是在供暖季节,其中有![]() 天为重度污染,完成
天为重度污染,完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为
的把握认为![]() 市本年度空气重度污染与供暖有关?
市本年度空气重度污染与供暖有关?

下面临界值表供参考.
| 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() .
.