题目内容
【题目】
总决赛采用7场4胜制，2018年总决赛两支球队分别为勇士和骑士，假设每场比赛勇士获胜的概率为0.7，骑士获胜的概率为0.3，且每场比赛的结果相互独立，则恰好5场比赛决出总冠军的概率为__________．
【答案】0.3108
【解析】分析：设“勇士以比分4：1获胜”为事件
，“第
场比赛取胜”记作事件
，由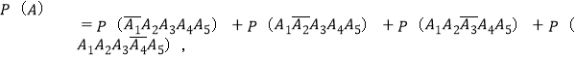
能求出勇士队以比分4：1获胜的概率．
设“骑士以比分4：1获胜”为事件
，“第场比赛取胜”记作事件
，由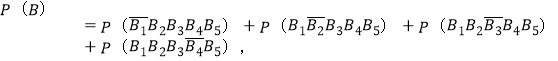
能求出骑士队以比分4：1获胜的概率．
则恰好5场比赛决出总冠军的概率为
.
详解：设“勇士以比分4：1获胜”为事件，“第场比赛取胜”记作事件，由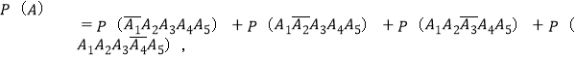
能求出勇士队以比分4：1获胜的概率．则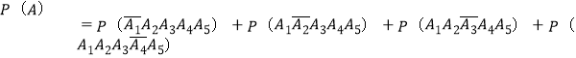
设“骑士以比分4：1获胜”为事件，“第场比赛取胜”记作事件，由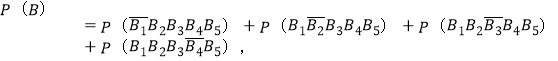
能求出骑士队以比分4：1获胜的概率．则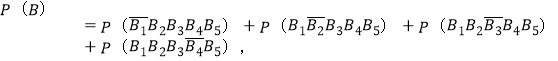
则恰好5场比赛决出总冠军的概率为
即答案为0.3108.
练习册系列答案
相关题目
【题目】某大学餐饮中心为了了解新生的饮食习惯，在某学院大一年级
名学生中进行了抽样调查，发现喜欢甜品的占
.这名学生中南方学生共
人。南方学生中有
人不喜欢甜品.
（1）完成下列
列联表：
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | |||
北方学生 | |||
合计 |
（2）根据表中数据，问是否有
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”；
（3）已知在被调查的南方学生中有
名数学系的学生，其中
名不喜欢甜品；有
名物理系的学生，其中
名不喜欢甜品.现从这两个系的学生中，各随机抽取人，记抽出的
人中不喜欢甜品的人数为
，求
的分布列和数学期望.
附：
.
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
