题目内容
已知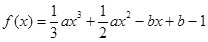 在
在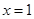 处的切线与
处的切线与 轴平行,若
轴平行,若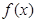 的图象经过四个象限,则实数
的图象经过四个象限,则实数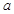 的取值范围是 。
的取值范围是 。
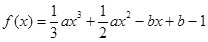 在
在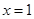 处的切线与
处的切线与 轴平行,若
轴平行,若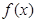 的图象经过四个象限,则实数
的图象经过四个象限,则实数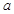 的取值范围是 。
的取值范围是 。(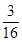 ,
,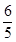 )
)
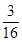 ,
,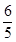 )
)因为求导函数可得f′(x)=ax2+ax-b
因为函数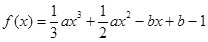 在x=1处的切线与x轴平行,
在x=1处的切线与x轴平行,
∴f′(1)=0∴2a-b=0∴b=2a∴f′(x)=ax2+ax-2a=a(x+2)(x-1),令f′(x)=a(x+2)(x-1)=0得x=-2或x=1
x∈(-∞,-2)时f′(x)的符号与x∈(-2,1)时f′(x)的符号相反,x∈(-2,1)时f′(x)的符号与x∈(1,+∞)时f′(x)的符号相反∴函数在-2与1处取极值∵图象经过四个象限∴f(-2)•f(1)<0,得到参数a的范围是(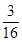 ,
,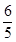 )
)
因为函数
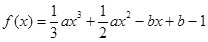 在x=1处的切线与x轴平行,
在x=1处的切线与x轴平行,∴f′(1)=0∴2a-b=0∴b=2a∴f′(x)=ax2+ax-2a=a(x+2)(x-1),令f′(x)=a(x+2)(x-1)=0得x=-2或x=1
x∈(-∞,-2)时f′(x)的符号与x∈(-2,1)时f′(x)的符号相反,x∈(-2,1)时f′(x)的符号与x∈(1,+∞)时f′(x)的符号相反∴函数在-2与1处取极值∵图象经过四个象限∴f(-2)•f(1)<0,得到参数a的范围是(
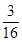 ,
,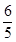 )
)
练习册系列答案
相关题目
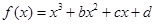 有两个极值点
有两个极值点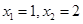 ,且直线
,且直线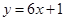 与曲线
与曲线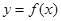 相切于
相切于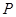 点.
点.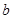 和
和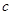
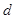 为整数时,求过
为整数时,求过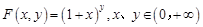 .
.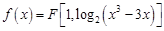 与直线
与直线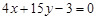 垂直的切线方程;
垂直的切线方程;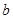 使曲线
使曲线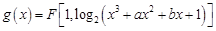 在
在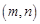 点处的切线斜率为
点处的切线斜率为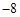 ,且
,且 ,求实数
,求实数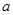 的取值范围.
的取值范围.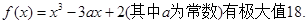
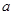 的值;
的值;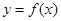 过原点的切线与函数
过原点的切线与函数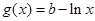 的图像有两个交点,试求b的取值范围.
的图像有两个交点,试求b的取值范围.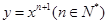 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为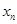 ,令
,令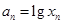 ,则
,则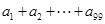 的值为
的值为 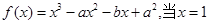 时,有极值10,则
时,有极值10,则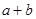 的值为
的值为 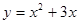 在点A(2,10)处的切线的斜率是
在点A(2,10)处的切线的斜率是 则
则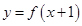 的单调减区间为( )
的单调减区间为( )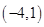
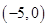
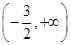
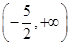
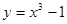 在x=1处的切线方程为 ( )
在x=1处的切线方程为 ( )