题目内容
【题目】下列命题中正确的有( )
①常数数列既是等差数列也是等比数列；②在
中，若
，则为直角三角形；③若
为锐角三角形的两个内角，则
；④若
为数列
的前
项和，则此数列的通项
.
A.①②B.②③C.③④D.①④
【答案】B
【解析】
根据等差（比）数列的定义，可判断①；根据正弦定理，可判断②；根据诱导公式及三角函数的单调性，可判断③；根据数列前
项和与通项公式的关系，可判断④.
对于①，每一项均为
的常数列是等差数列，不是等比数列，故①错误；
对于②，在
中，若
，则
，所以为直角三角形，故②正确；
对于③，因为
为锐角三角形的两个内角，所以
,即
，由函数
在
单调增，可得
，即
，同理可得
，所以
，故③正确；
对于④，若
为数列
的前项和，则此数列的通项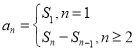
，故④错误.
故选：B.
【题目】下表是某地一家超市在2018年一月份某一周内周2到周6的时间
与每天获得的利润
（单位：万元）的有关数据．
星期 | 星期2 | 星期3 | 星期4 | 星期5 | 星期6 |
利润 | 2 | 3 | 5 | 6 | 9 |
（1）根据上表提供的数据，用最小二乘法求线性回归直线方程
；
（2）估计星期日获得的利润为多少万元．
参考公式： 
【题目】某种工业机器生产商，对一次性购买2台机器的客户，推出两种超过质保期后两年内的延保维修优惠方案：
方案一：交纳延保金700元，在延保的两年内可免费维修2次，超过2次每次收取维修费200元；
方案二：交纳延保金1000元，在延保的两年内可免费维修4次，超过4次每次收取维修费100元．
某工厂准备一次性购买2台这种机器．现需决策在购买机器时应购买哪种延保方案，为此搜集并整理了50台这种机器超过质保期后延保两年内维修的次数，得下表：
维修次数 | 0 | 1 | 2 | 3 |
台数 | 5 | 20 | 10 | 15 |
以这50台机器维修次数的频率代替1台机器维修次数发生的概率．记X表示这2台机器超过质保期后延保的两年内共需维修的次数．
（1）求X的分布列；
（2）以所需延保金及维修费用的期望值为决策依据，工厂选择哪种延保方案更合算？
