题目内容
(本小题12分) 已知曲线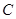
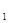 的极坐标方程为
的极坐标方程为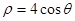 ,曲线
,曲线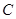
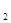 的方程是
的方程是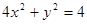 , 直线
, 直线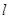 的参数方程是:
的参数方程是: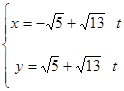
 .
.
(1)求曲线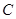
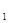 的直角坐标方程,直线
的直角坐标方程,直线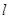 的普通方程;
的普通方程;
(2)求曲线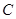
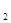 上的点到直线
上的点到直线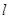 距离的最小值.
距离的最小值.
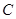
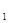 的极坐标方程为
的极坐标方程为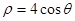 ,曲线
,曲线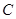
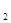 的方程是
的方程是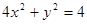 , 直线
, 直线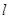 的参数方程是:
的参数方程是: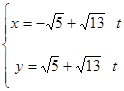
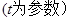 .
.(1)求曲线
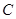
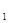 的直角坐标方程,直线
的直角坐标方程,直线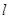 的普通方程;
的普通方程;(2)求曲线
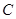
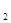 上的点到直线
上的点到直线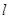 距离的最小值.
距离的最小值. 解: (1) 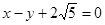 ;(2)到直线
;(2)到直线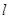 距离的最小值为
距离的最小值为 。
。
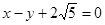 ;(2)到直线
;(2)到直线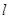 距离的最小值为
距离的最小值为 。
。 试题分析:(Ⅰ)利用直角坐标与极坐标间的关系:ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得C的直角坐标方程,将直线l的参数消去得出直线l的普通方程.
(Ⅱ)曲线C1的方程为4x2+y2=4,设曲线C1上的任意点(cosθ,2sinθ),利用点到直线距离公式,建立关于θ的三角函数式求解.
解: (1) 曲线
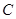
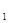 的方程为
的方程为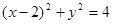 ,直线
,直线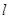 的方程是:
的方程是: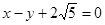
(2)设曲线
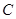
 上的任意点
上的任意点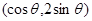 ,
, 该点到直线
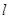 距离
距离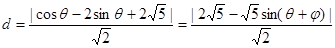 .
. 到直线
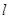 距离的最小值为
距离的最小值为 。
。 点评:解决该试题的关键是对于椭圆上点到直线距离的最值问题,一般用参数方程来求解得到。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
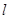 的参数方程为
的参数方程为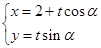 ,(
,(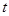 为参数,
为参数,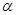 为倾斜角,且
为倾斜角,且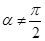 )与曲线
)与曲线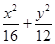 =1交于
=1交于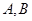 两点.
两点.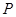 的坐标;
的坐标;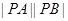 的最大值。
的最大值。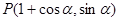 ,参数
,参数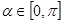
 ,点Q在曲线C:
,点Q在曲线C: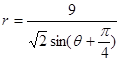 上.
上.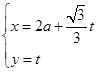 (
(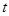 为参数,
为参数,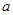 为常数且
为常数且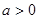 )被以原点为极点,
)被以原点为极点,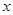 轴的正半轴为极轴,方程为
轴的正半轴为极轴,方程为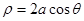 的曲线所截,求截得的弦长.
的曲线所截,求截得的弦长.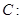
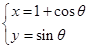 (
(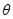 为参数)和直线
为参数)和直线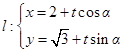 (其中为参数,
(其中为参数, 为直线的倾斜角),如果直线与圆
为直线的倾斜角),如果直线与圆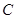 有公共点,求
有公共点,求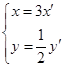
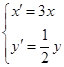
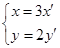
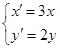
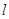 的参数方程为
的参数方程为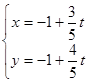
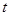 为参数).若以坐标原点
为参数).若以坐标原点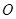 为极点,
为极点,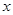 轴正半轴为极轴建立极坐标系,则曲线
轴正半轴为极轴建立极坐标系,则曲线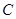 的极坐标方程为
的极坐标方程为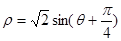 .
.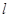 方程是
方程是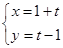
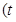 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,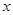 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆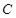 的极坐标方程为
的极坐标方程为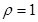 ,则圆
,则圆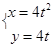 (t为参数)上,则
(t为参数)上,则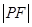 =( )
=( )