题目内容
(坐标系与参数方程选做题) 已知直线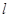 方程是
方程是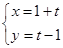
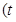 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,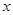 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆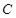 的极坐标方程为
的极坐标方程为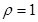 ,则圆
,则圆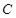 上的点到直线
上的点到直线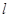 的距离最小值是
的距离最小值是
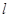 方程是
方程是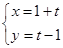
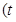 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,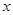 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆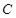 的极坐标方程为
的极坐标方程为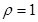 ,则圆
,则圆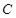 上的点到直线
上的点到直线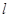 的距离最小值是
的距离最小值是 
解:直线l的参数方程为x="1+t," y="t-1," (参数t∈R),消去t的普通方程为 x-y-2=0,
∵圆C的极坐标方程为ρ=1
∴圆C的普通方程为 x2+y2=1,圆心(0,0),半径为1,
则圆心C到直线l的距离为d= ,圆C上的点到直线l的距离最小值是d-r=
,圆C上的点到直线l的距离最小值是d-r=
故答案为
∵圆C的极坐标方程为ρ=1
∴圆C的普通方程为 x2+y2=1,圆心(0,0),半径为1,
则圆心C到直线l的距离为d=
 ,圆C上的点到直线l的距离最小值是d-r=
,圆C上的点到直线l的距离最小值是d-r=
故答案为


练习册系列答案
相关题目
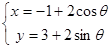 (
(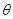 为参数),直线的方程为
为参数),直线的方程为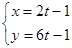 (t为参数),则直线与圆的位置关系是( )。
(t为参数),则直线与圆的位置关系是( )。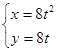 (
(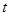 为参数),焦点为
为参数),焦点为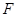 ,准线为
,准线为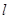 ,
,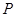 为抛物线上一点,
为抛物线上一点,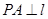 ,
,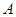 为垂足,如果直线
为垂足,如果直线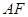 的斜率为
的斜率为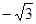 ,那么
,那么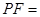 。
。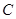
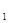 的极坐标方程为
的极坐标方程为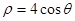 ,曲线
,曲线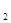 的方程是
的方程是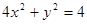 , 直线
, 直线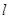 的参数方程是:
的参数方程是: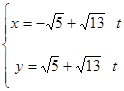
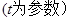 .
.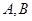 的坐标分别为
的坐标分别为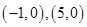 ,直线
,直线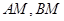 相交于点
相交于点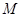 ,且它们的斜率之积是
,且它们的斜率之积是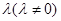 ,试讨论点
,试讨论点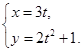 (
(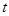 为参数),则过曲线C上横坐标为1的点的切线方程为 .
为参数),则过曲线C上横坐标为1的点的切线方程为 .
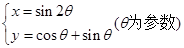 上的点是
上的点是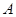 .
.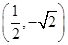
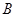 .
.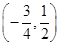
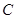 .
.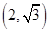
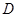 .
.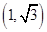
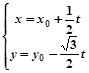 (t为参数),则此直线的倾斜角为 _______.
(t为参数),则此直线的倾斜角为 _______.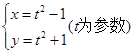 表示的曲线是( )
表示的曲线是( )