题目内容
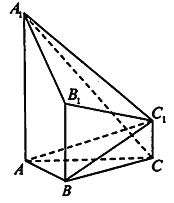
【题目】如图, ![]() ,
, ![]() 为
为![]() 中点,且
中点,且![]() 平面
平面![]() ,
, ![]() .已知
.已知![]() .
.
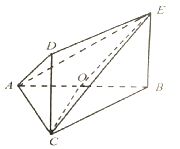
(1)求直线![]() 与
与![]() 所成角;
所成角;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由![]() 且
且![]() 平面
平面![]() ,建立以
,建立以![]() 为原点,
为原点, ![]() 为
为![]() 轴正方向,
轴正方向, ![]() 为
为![]() 轴正方向,
轴正方向, ![]() 为
为![]() 轴正方向的空间直角坐标系,再根据
轴正方向的空间直角坐标系,再根据![]() ,得出
,得出![]() 与
与![]() ,从而可求出直线
,从而可求出直线![]() 与
与![]() 所成角;(2)分别求出平面
所成角;(2)分别求出平面![]() 和平面
和平面![]() 的一个法向量,求出两法向量所成角的余弦值,可得二面角
的一个法向量,求出两法向量所成角的余弦值,可得二面角![]() 的余弦值.
的余弦值.
试题解析:(1)因为![]() 且
且![]() 平面
平面![]() ,则以
,则以![]() 为原点,
为原点, ![]() 为
为![]() 轴正方向,
轴正方向, ![]() 为
为![]() 轴正方向,
轴正方向, ![]() 为
为![]() 轴正方向,建立如图所示的空间直角坐标系.
轴正方向,建立如图所示的空间直角坐标系.
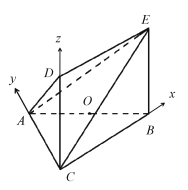
∵![]()
∴![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() .
.
∴![]() ,
, 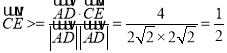 .
.
∴![]() 和
和![]() 的夹角为
的夹角为![]() .
.
(2)平面![]() 的法向量
的法向量![]() ,设平面
,设平面![]() 的法向量
的法向量![]() .
.
由![]() ,
, ![]() 且
且![]() ,
, ![]() ,
,
得![]() ,则
,则![]() ,解得
,解得![]() ,
,
取![]() ,则
,则![]() .
.
∵二面角![]() 为锐二面角,记为
为锐二面角,记为![]()
∴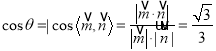 .
.
点晴:本题主要考查利用空间向量求二面角,利用空间向量求异面直线所成的角,属于难题. 空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目