题目内容
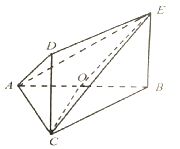
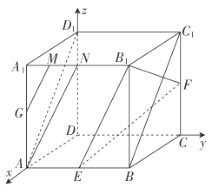
【题目】如图,在正方体![]() 中,
中,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,
的中点,![]() 为棱
为棱![]() 上一点,
上一点,![]() 且
且![]() 平面
平面![]() .
.
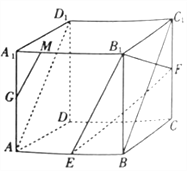
(1)证明:![]() 为
为![]() 中点;
中点;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)见解析;(2)锐二面角的余弦值为![]() .
.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,利用
,利用![]() ,
,![]() 证得四边形
证得四边形![]() 为平行四边形,则
为平行四边形,则![]() ,所以
,所以![]() 为
为![]() 的中点;
的中点;
(2)以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() .不妨令正方体的棱长为2,利用两个面的法向量求解即可.
.不妨令正方体的棱长为2,利用两个面的法向量求解即可.
试题解析:
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,因为
,因为![]() ,所以
,所以![]() 为
为![]() 的中点,又
的中点,又![]() 为
为![]() 的中点,所以
的中点,所以![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() ,即
,即![]() ,又
,又![]() ,所以四边形
,所以四边形![]() 为平行四边形,则
为平行四边形,则![]() ,所以
,所以![]() 为
为![]() 的中点.
的中点.
(2)解:以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() .不妨令正方体的棱长为2,则
.不妨令正方体的棱长为2,则![]() ,可得
,可得![]() ,
,![]() ,设
,设![]() 是平面
是平面![]() 的法向量,则
的法向量,则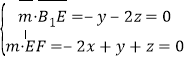 .令
.令![]() ,得
,得![]() .
.
易得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以![]()
![]() .
.
故所求锐二面角的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额如下表:
商店名称 | A | B | C | D | E |
销售额x/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图,观察散点图,说明两个变量是否线性相关;
(2)用最小二乘法计算利润额y对销售额x的线性回归方程;
(3)当销售额为4千万元时,估计利润额的大小.
(参考公式: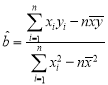 ,
,![]() )
)