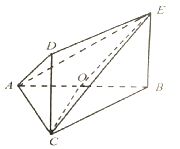
题目内容
【题目】已知抛物线![]() 的焦点到直线
的焦点到直线![]() 的距离为
的距离为![]() .
.
(1)求抛物线的标准方程;
(2)设点![]() 是抛物线上的动点,若以点
是抛物线上的动点,若以点![]() 为圆心的圆在
为圆心的圆在![]() 轴上截得的弦长均为4,求证:圆
轴上截得的弦长均为4,求证:圆![]() 恒过定点.
恒过定点.
【答案】(1) ![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:
(1)由题意可得抛物线的焦点坐标为![]() ,利用点到直线距离公式得到关于实数p的方程,解方程可得抛物线的标准方程是
,利用点到直线距离公式得到关于实数p的方程,解方程可得抛物线的标准方程是![]() .
.
(2)设圆心![]() 的坐标为
的坐标为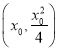 ,半径为
,半径为![]() ,由题意结合勾股定理有
,由题意结合勾股定理有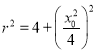 ,则圆
,则圆![]() 的标准方程整理变形可得
的标准方程整理变形可得![]() ,该方程对于任意的
,该方程对于任意的![]() 均成立,则
均成立,则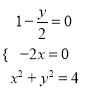 据此可得圆
据此可得圆![]() 过一定点为
过一定点为![]() .
.
试题解析:
(1)由题意, ![]() ,焦点坐标为
,焦点坐标为![]() ,
,
由点到直线的距离公式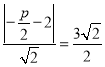 ,得
,得![]() ,
,
所以抛物线的标准方程是![]() .
.
(2)设圆心![]() 的坐标为
的坐标为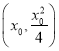 ,半径为
,半径为![]() ,圆
,圆![]() 在
在![]() 轴上截得的弦长为
轴上截得的弦长为![]() ,
,
所以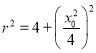 ,
,
圆![]() 的标准方程:
的标准方程: 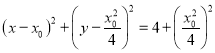 ,
,
化简得: ![]() ,①
,①
对于任意的![]() ,方程①均成立,
,方程①均成立,
故有: 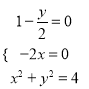 解得:
解得: ![]() ,所以,圆
,所以,圆![]() 过一定点为
过一定点为![]() .
.

练习册系列答案
相关题目
【题目】已知某运动员每次投篮命中的概率为80%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4,5,6,7,8表示命中,9,0表示未命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 | 966 | 191 | 925 | 271 | 932 | 812 | 458 | 569 | 683 |
431 | 257 | 393 | 027 | 556 | 488 | 730 | 113 | 537 | 989 |
据此估计,该运动员三次投篮均命中的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()