题目内容
【题目】设命题p:x0∈(1,+∞),使得5+|x0|=6.q:x∈(0,+∞),![]() +81x≥a.
+81x≥a.
(1)若a=9,判断命题¬p,p∨q,(¬p)∧(¬q)的真假,并说明理由;
(2)设命题r:x0∈R,x02+2x0+a-9≤0判断r成立是q成立的什么条件,并说明理由.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)命题p根据不等式定义即可得出真假;命题q可根据均值不等式进行判断.
(2)根据一元二次方程![]() 属性判断a值范围,并与命题q进行比较,遂可得解.
属性判断a值范围,并与命题q进行比较,遂可得解.
解:(1)若![]() ,则
,则![]() >1,则5+
>1,则5+![]() >6,即命题p为假,¬p为真,
>6,即命题p为假,¬p为真,
当x>0时,由均值不等式得:![]() +81x≥2
+81x≥2![]() =9(当且仅当
=9(当且仅当![]() =81x即x=
=81x即x=![]() 时取等号)
时取等号)
又a=9,即命题q为真,¬q为假,
故¬p为真命题,p∨q为真命题,(¬p)∧(¬q)为假命题.
(2)由命题r:x0∈R,x02+2x0+a-9≤0为真,
即△=4-4(a-9)≥0,
解得:a≤10,
由(1)得,当q为真时,a≤9,
又“a≤10“是”a≤9“的必要不充分条件,
故r成立是q成立的必要不充分条件.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额如下表:
商店名称 | A | B | C | D | E |
销售额x/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图,观察散点图,说明两个变量是否线性相关;
(2)用最小二乘法计算利润额y对销售额x的线性回归方程;
(3)当销售额为4千万元时,估计利润额的大小.
(参考公式: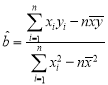 ,
,![]() )
)