题目内容
9.已知$\underset{lim}{n→∞}$(2n+1)an=1,求$\underset{lim}{n→∞}$nan.分析 通过$\underset{lim}{n→∞}$(2n+1)的极限不存在及$\underset{lim}{n→∞}$(2n+1)an=1可知$\underset{lim}{n→∞}$$\frac{1}{{a}_{n}}$的极限也不存在,利用洛必达法则计算可知$\underset{lim}{n→∞}$$(\frac{1}{{a}_{n}})′$=2,进而计算可得结论.
解答 解:∵$\underset{lim}{n→∞}$(2n+1)an=$\underset{lim}{n→∞}$$\frac{2n+1}{\frac{1}{{a}_{n}}}$
=$\underset{lim}{n→∞}$$\frac{2}{(\frac{1}{{a}_{n}})′}$
=$\frac{2}{\underset{lim}{n→∞}(\frac{1}{{a}_{n}})′}$
=1,
∴$\underset{lim}{n→∞}$$(\frac{1}{{a}_{n}})′$=2,
∴$\underset{lim}{n→∞}$nan=$\underset{lim}{n→∞}$$\frac{n}{\frac{1}{{a}_{n}}}$
=$\underset{lim}{n→∞}$$\frac{1}{(\frac{1}{{a}_{n}})′}$
=$\frac{1}{\underset{lim}{n→∞}(\frac{1}{{a}_{n}})′}$
=$\frac{1}{2}$.
点评 本题考查数列极限及其运算,利用洛必达法则是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
19.若曲线f(x)=$\frac{1}{3}$ax3+$\frac{1}{2}$bx2+cx+d(a,b,c>0)上不存在斜率为0的切线,则$\frac{f′(1)}{b}$-1的取值范围是( )
| A. | (1,+∞) | B. | [1,+∞) | C. | (2,+∞) | D. | [2,+∞) |
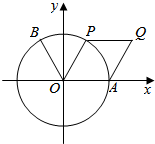 如图,点B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),点A时单位圆与x轴正半轴的交点.设点P为单位圆上的动点,点Q满足$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$,∠AOP=2θ($\frac{π}{6}$≤θ<$\frac{π}{2}$),f(θ)=$\overrightarrow{OB}$•$\overrightarrow{OQ}$,求f(θ)的取值范围,当$\overrightarrow{OB}$⊥$\overrightarrow{OQ}$时,求四边形OAQP的面积.
如图,点B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),点A时单位圆与x轴正半轴的交点.设点P为单位圆上的动点,点Q满足$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$,∠AOP=2θ($\frac{π}{6}$≤θ<$\frac{π}{2}$),f(θ)=$\overrightarrow{OB}$•$\overrightarrow{OQ}$,求f(θ)的取值范围,当$\overrightarrow{OB}$⊥$\overrightarrow{OQ}$时,求四边形OAQP的面积.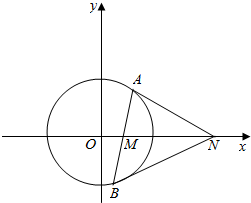 如图,已知圆O:x2+y2=r2(r>0),动直线l过点M(1,0)交圆O于A(x1,y1),B(x2,y2)两点(点A在x轴上方),点N在x轴上,若点B的坐标为(0,-r),则点A的横坐标为$\frac{8}{5}$.
如图,已知圆O:x2+y2=r2(r>0),动直线l过点M(1,0)交圆O于A(x1,y1),B(x2,y2)两点(点A在x轴上方),点N在x轴上,若点B的坐标为(0,-r),则点A的横坐标为$\frac{8}{5}$.