题目内容
19.若曲线f(x)=$\frac{1}{3}$ax3+$\frac{1}{2}$bx2+cx+d(a,b,c>0)上不存在斜率为0的切线,则$\frac{f′(1)}{b}$-1的取值范围是( )| A. | (1,+∞) | B. | [1,+∞) | C. | (2,+∞) | D. | [2,+∞) |
分析 由题意得到f′(x)=ax2+bx+c=0无解,即b<2$\sqrt{ac}$,因为$\frac{f′(1)}{b}$-1=$\frac{a+c}{b}$,利用基本不等式即可求出.
解答 解:∵曲线f(x)上不存在斜率为0的切线,
∴f′(x)=ax2+bx+c=0无解,
∴△=b2-4ac<0,即b<2$\sqrt{ac}$
∴f′(1)=a+b+c,
∴$\frac{f′(1)}{b}$-1=$\frac{a+b+c}{b}$-1=$\frac{a+c}{b}$,
∵$\frac{a+c}{b}$≥$\frac{2\sqrt{ac}}{b}$≥$\frac{b}{b}$=1,
∴$\frac{f′(1)}{b}$-1的取值范围是[1,+∞),
故选:B.
点评 本题考查了导数的运算法则和方程的解得问题,以及基本不等式,属于基础题.

练习册系列答案
相关题目
11.设A={x|x=2k+1,k∈Z},B={x|x=2(k+1),k∈Z},C={x|x=2k-1,k∈N},D={x|x=2(k-1),k∈Z},则A、B、C、D中相等的集合有( )
| A. | A=C且B=D | B. | B=D | C. | A=C | D. | A=B=D |
7.若tanθ=$\frac{1}{3}$,则2cos2θ+sin2θ的值是( )
| A. | $\frac{12}{5}$ | B. | $\frac{8}{5}$ | C. | -$\frac{8}{5}$ | D. | -$\frac{12}{5}$ |
4.函数y=ln(x2)+x3的图象大致是( )
| A. | 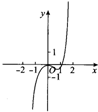 | B. | 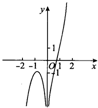 | C. | 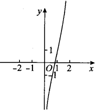 | D. | 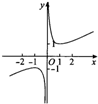 |