题目内容
4.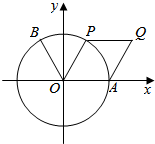 如图,点B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),点A时单位圆与x轴正半轴的交点.设点P为单位圆上的动点,点Q满足$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$,∠AOP=2θ($\frac{π}{6}$≤θ<$\frac{π}{2}$),f(θ)=$\overrightarrow{OB}$•$\overrightarrow{OQ}$,求f(θ)的取值范围,当$\overrightarrow{OB}$⊥$\overrightarrow{OQ}$时,求四边形OAQP的面积.
如图,点B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),点A时单位圆与x轴正半轴的交点.设点P为单位圆上的动点,点Q满足$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$,∠AOP=2θ($\frac{π}{6}$≤θ<$\frac{π}{2}$),f(θ)=$\overrightarrow{OB}$•$\overrightarrow{OQ}$,求f(θ)的取值范围,当$\overrightarrow{OB}$⊥$\overrightarrow{OQ}$时,求四边形OAQP的面积.
分析 由题意可得P(cos2θ,sin2θ),A(1,0),再由$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$得到$\overrightarrow{OQ}$的坐标,再由数量积的坐标运算求得f(θ),然后由θ得范围求得f(θ)的范围;然后由
$\overrightarrow{OB}$⊥$\overrightarrow{OQ}$求得θ值,则四边形OAQP的面积可求.
解答 解:由题意可得:P(cos2θ,sin2θ),A(1,0),
则$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$=(1+cos2θ,sin2θ),
又∵B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
∴f(θ)=$\overrightarrow{OB}$•$\overrightarrow{OQ}$=-$\frac{1}{2}$(1+cos2θ)+$\frac{\sqrt{3}}{2}$sin2θ
=sin(2θ-$\frac{π}{6}$)-$\frac{1}{2}$,
∵$\frac{π}{6}$≤θ<$\frac{π}{2}$,
∴$\frac{π}{6}$≤2θ-$\frac{π}{6}$<$\frac{5π}{6}$,则$\frac{1}{2}$≤sin(2θ-$\frac{π}{6}$)≤1,
∴0≤f(θ)≤$\frac{1}{2}$,
∴f(θ)的取值范围[0,$\frac{1}{2}$].
当$\overrightarrow{OB}$⊥$\overrightarrow{OQ}$时,有sin(2θ-$\frac{π}{6}$)-$\frac{1}{2}$=0,
即sin(2θ-$\frac{π}{6}$)=$\frac{1}{2}$,
∵$\frac{π}{6}$≤2θ-$\frac{π}{6}$<$\frac{5π}{6}$,∴2θ-$\frac{π}{6}$=$\frac{π}{6}$,
解得:$θ=\frac{π}{6}$.
∴${S}_{四边形OAQP}=2×\frac{1}{2}×1×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}$.
点评 本题考查三角函数的定义、二倍角公式、两角差的正弦公式等三角函数的知识,考查了运算求解能力、化归与转化思想,是中档题.

| A. | 函数y=f(x)为R上的可导函数,则f'(x0)=0是x0为函数f(x)极值点的充要条件. | |
| B. | 若命题p:?x°∈R,x°2-x°+1<0,则?p:?x∈R,x2-x+1>0 | |
| C. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 | |
| D. | “已知不等式$\frac{1}{x}+\frac{9}{y}$>$\frac{k}{x+y}$对任意正数x、y恒成立”的充要条件为“k<16” |