题目内容
【题目】已知二次函数f(x)=ax2+bx(a,b为常数,且a≠0)满足条件:f(x﹣1)=f(3﹣x)且方程f(x)=2x有两个相等实数根 (Ⅰ)求f(x)的解析式;
(Ⅱ)是否存在实数m,n(m<n),使f(x)的定义域和值域分别为[m,n]和[4m,4n],如果存在,求出符合条件的所有m,n的值,如果不存在,说明理由.
【答案】解:(Ⅰ)∵f(﹣x+3)=f(x﹣1),
∴对称轴是x=1,
得到﹣ ![]() =1 ①
=1 ①
∵方程f(x)=2x有两个相等的实数根,
即ax2+(b﹣2)x=0有两个相等的实数根,
∴△=(b﹣2)2=0,∴b=2,代入①,
解得a=﹣1,
∴f(x)=﹣x2+2x;
(Ⅱ)∵f(x)=﹣(x﹣1)2+1≤1,
∴4n≤1,即n≤ ![]() ,
,
而抛物线y=﹣x2+2x的对称轴为x=1,
∴当n≤ ![]() 时,f(x)在[m,n]上为增函数.
时,f(x)在[m,n]上为增函数.
若满足题设条件的m,n存在,
则 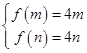 ,即
,即 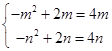
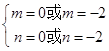 又m<n≤
又m<n≤ ![]() .
.
∴m=﹣2,n=0,这时,定义域为[﹣2,0],值域为[﹣8,0].
由以上知满足条件的m,n存在,m=﹣2,n=0
【解析】(Ⅰ)由方程ax2+bx﹣2x=0有等根,则△=0,得b,又由f(x﹣1)=f(3﹣x)知此函数图象的对称轴方程为x=﹣ ![]() =1,得a,从而求得f(x).(Ⅱ)由f(x)=﹣(x﹣1)2+1≤1,知4n≤1,即n≤
=1,得a,从而求得f(x).(Ⅱ)由f(x)=﹣(x﹣1)2+1≤1,知4n≤1,即n≤ ![]() .由对称轴为x=1,知当n≤
.由对称轴为x=1,知当n≤ ![]() 时,f(x)在[m,n]上为增函数,得到关于m,n的方程组,最后看是否满足m<n≤
时,f(x)在[m,n]上为增函数,得到关于m,n的方程组,最后看是否满足m<n≤ ![]() 即可.
即可.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案