题目内容
19.函数f(x)是(0,+∞)上单调递增函数,当n∈N*时,f(n)∈N*,且f[f(n)]=3n,则f(3n)的值等于2•3n.分析 由已知中函数f(x)是(0,+∞)上单调递增函数,当n∈N*时,f(n)∈N*,且f[f(n)]=3n,可得f(1)=2,f(3)=6,f(9)=18,f(27)=54,归纳可得答案.
解答 解:∵f(x)在(0,+∞)上是单调增函数,f[f(n)]=3n
∴f(f(1))=3,且f(1)≠1 (若f(1)=1,则f(f(1))=f(1)=3,与f(1)=1矛盾)
∵f(x)∈N*
∴f(1)≥2
∴f(2)≤f(f(1)),∵f(f(1))=3,∴f(2)≤3,
故f(1)=2,f(2)=3,
∴f(3)=f(f(2))=6,
∴f(6)=f(f(3))=9,
∴f(9)=f(f(6))=18,
∴f(18)=f(f(9))=27,
∴f(27)=f(f(18))=54,
…
归纳可得:f(3n)=2•3n,
故答案为:2•3n
点评 本题考查函数的单调性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
9.已知正四棱柱(底面为正方形,侧棱垂直于底面的四棱柱)ABCD-A1B1C1D1中,AA1=$\sqrt{2}$AB,E为AA1中点,则异面直线BE与C1D所成角的余弦为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{{3\sqrt{10}}}{10}$ | D. | 0 |
10.已知学生的数学成绩与物理成绩具有线性相关关系,某班6名学生的数学和物理成绩如表:
(1)求物理成绩y对数学成绩x的线性回归方程;
(2)当某位学生的数学成绩为70分时,预测他的物理成绩.
参考公式:用最小二乘法求线性回归方程$\widehat{y}=\widehat{b}x+\widehat{a}$的系数公式:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}=\overline{y}-a\overline{x}$.
参考数据:832+782+732+682+632+732=32224,
83×75+78×65+73×75+68×65+63×60+73×80=30810.
 | A | B | C | D | E | F |
| 数学成绩(x) | 83 | 78 | 73 | 68 | 63 | 73 |
| 物理成绩(y) | 75 | 65 | 75 | 65 | 60 | 80 |
(2)当某位学生的数学成绩为70分时,预测他的物理成绩.
参考公式:用最小二乘法求线性回归方程$\widehat{y}=\widehat{b}x+\widehat{a}$的系数公式:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}=\overline{y}-a\overline{x}$.
参考数据:832+782+732+682+632+732=32224,
83×75+78×65+73×75+68×65+63×60+73×80=30810.
3.已知等差数列{an}的公差d≠0,且a1,a5,a17依次成等比,则这个等比数列的公比是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | 3 |
20.已知函数f(x)=$\left\{\begin{array}{l}(3a-1)x+4a,x<1\\{a^x}-a,x≥1\end{array}$,且f′(x)<0在(-∞,+∞)上恒成立,那么a的取值范围是( )
| A. | (0,1) | B. | (0,$\frac{1}{3}$) | C. | [$\frac{1}{7}$,$\frac{1}{3}$) | D. | [$\frac{1}{7}$,1) |
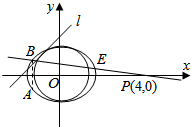 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,以原点为圆心、椭圆的短半径为半径的圆与直线l:x-y+$\sqrt{6}$=0相切.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,以原点为圆心、椭圆的短半径为半径的圆与直线l:x-y+$\sqrt{6}$=0相切.