题目内容
9.已知正四棱柱(底面为正方形,侧棱垂直于底面的四棱柱)ABCD-A1B1C1D1中,AA1=$\sqrt{2}$AB,E为AA1中点,则异面直线BE与C1D所成角的余弦为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{{3\sqrt{10}}}{10}$ | D. | 0 |
分析 以DA,DC,DD1三直线分别为x,y,z轴,建立空间直角坐标系,可设AB=1,这样便可求出B,E,D,C1几点的坐标,从而会得出$\overrightarrow{BE}=(0,-1,\frac{\sqrt{2}}{2}),\overrightarrow{{C}_{1}D}=(0,-1,-\sqrt{2})$,这样便有$\overrightarrow{BE}•\overrightarrow{{C}_{1}D}=0$,从而得出异面直线BE与C1D所成角的余弦值为0.
解答 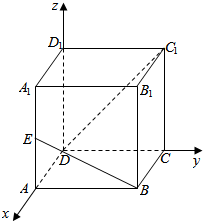 解:如图,分别以边DA,DC,DD1所在直线为x,y,z轴,建立空间直角坐标系,设AB=1,则:
解:如图,分别以边DA,DC,DD1所在直线为x,y,z轴,建立空间直角坐标系,设AB=1,则:
D(0,0,0),${C}_{1}(0,1,\sqrt{2})$,B(1,1,0),$E(1,0,\frac{\sqrt{2}}{2})$;
∴$\overrightarrow{BE}=(0,-1,\frac{\sqrt{2}}{2})$,$\overrightarrow{{C}_{1}D}=(0,-1,-\sqrt{2})$;
∴$\overrightarrow{BE}•\overrightarrow{{C}_{1}D}=0$;
∴$\overrightarrow{BE}⊥\overrightarrow{{C}_{1}D}$;
∴异面直线BE与C1D所成角为90°,其余弦值为0.
故选:D.
点评 考查建立空间直角坐标系,利用空间向量求异面直线所成角的余弦值的方法,能求空间点的坐标,根据点的坐标求向量坐标,以及非零向量垂直的充要条件.

练习册系列答案
相关题目
20.复平面内表示复数i(1-2i)的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.已知z为纯虚数,$\frac{z+2}{1-i}$是实数,则复数z=( )
| A. | 2i | B. | i | C. | -2i | D. | -i |
