题目内容
【题目】(1)已知命题![]() :实数
:实数![]() 满足
满足![]() ,命题
,命题![]() :实数
:实数![]() 满足方程
满足方程![]() 表示的焦点在
表示的焦点在![]() 轴上的椭圆,且
轴上的椭圆,且![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围;
的取值范围;
(2)设命题![]() :关于
:关于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ;
;![]() :函数
:函数![]() 的定义域为
的定义域为![]() .若
.若![]() 是真命题,
是真命题,![]() 是假命题,求实数
是假命题,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1)利用一元二次不等式的解法化简![]() ,利用椭圆的标准方程化简
,利用椭圆的标准方程化简![]() ,由包含关系列不等式求解即可;(2)化简命题
,由包含关系列不等式求解即可;(2)化简命题![]() 可得
可得![]() ,化简命题
,化简命题![]() 可得
可得![]() ,由
,由![]() 为真命题,
为真命题,![]() 为假命题,可得
为假命题,可得![]() 一真一假,分两种情况讨论,对于
一真一假,分两种情况讨论,对于![]() 真
真![]() 假以及
假以及![]() 假
假![]() 真分别列不等式组,分别解不等式组,然后求并集即可求得实数
真分别列不等式组,分别解不等式组,然后求并集即可求得实数![]() 的取值范围.
的取值范围.
详解:(1)由![]() 得:
得:![]() ,即命题
,即命题![]()
由![]() 表示焦点在
表示焦点在![]() 轴上的椭圆,可得
轴上的椭圆,可得![]() ,解得
,解得![]() ,即命题
,即命题![]() .
.
因为![]() 是
是![]() 的充分不必要条件,所以
的充分不必要条件,所以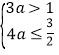 或
或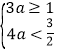
解得:![]() ,∴实数
,∴实数![]() 的取值范围是
的取值范围是![]() .
.
(2)解:命题![]() 为真命题时,实数
为真命题时,实数![]() 的取值集合为
的取值集合为![]()
对于命题![]() :函数
:函数![]() 的定义域为
的定义域为![]() 的充要条件是
的充要条件是![]() ①恒成立.
①恒成立.
当![]() 时,不等式①为
时,不等式①为![]() ,显然不成立;
,显然不成立;
当![]() 时,不等式①恒成立的条件是
时,不等式①恒成立的条件是![]() ,解得
,解得![]()
所以命题![]() 为真命题时,
为真命题时,![]() 的取值集合为
的取值集合为![]()
由“![]() 是真命题,
是真命题,![]() 是假命题”,可知命题
是假命题”,可知命题![]() 、
、![]() 一真一假
一真一假
当![]() 真
真![]() 假时,
假时,![]() 的取值范围是
的取值范围是![]()
当![]() 假
假![]() 真时,
真时,![]() 的取值范围是
的取值范围是![]()
综上,![]() 的取值范围是
的取值范围是![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某工厂为了对研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价 | 9 | 9.2 | 9.4 | 9.6 | 9.8 | 10 |
销量 | 100 | 94 | 93 | 90 | 85 | 78 |
(1)若销量![]() 与单价
与单价![]() 服从线性相关关系,求该回归方程;
服从线性相关关系,求该回归方程;
(2)在(1)的前提下,若该产品的成本是5元/件,问:产品该如何确定单价,可使工厂获得最大利润。
附:对于一组数据![]() ,
,![]() ,……
,……![]() ,
,
其回归直线![]() 的斜率的最小二乘估计值为
的斜率的最小二乘估计值为 ;
;
本题参考数值:![]() .
.
【题目】某市为提高市民的戒烟意识,通过一个戒烟组织面向全市烟民征招志愿戒烟者,从符合条件的志愿者中随机抽取100名,将年龄分成![]() ,
,![]() ,
,![]() ,
,![]() ,
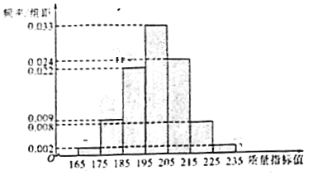
,![]() 五组,得到频率分布直方图如图所示.
五组,得到频率分布直方图如图所示.

(1)求图中![]() 的值,并估计这100名志愿者的平均年龄(同一组中的数据用该组区间的中点值作代表);
的值,并估计这100名志愿者的平均年龄(同一组中的数据用该组区间的中点值作代表);
(2)若年龄在![]() 的志愿者中有2名女性烟民,现从年龄在
的志愿者中有2名女性烟民,现从年龄在![]() 的志愿者中随机抽取2人,求至少有一名女性烟民的概率;
的志愿者中随机抽取2人,求至少有一名女性烟民的概率;
(3)该戒烟组织向志愿者推荐了![]() ,
,![]() 两种戒烟方案,这100名志愿者自愿选取戒烟方案,并将戒烟效果进行统计如下:
两种戒烟方案,这100名志愿者自愿选取戒烟方案,并将戒烟效果进行统计如下:
有效 | 无效 | 合计 | |
方案 | 48 | 60 | |
方案 | 36 | ||
合计 |
完成上面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为戒烟方案是否有效与方案选取有关.
的把握认为戒烟方案是否有效与方案选取有关.
参考公式:![]() ,
,![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |