ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ¥”Ρ≥Τσ“Β…ζ≤ζΒΡΡ≥÷÷≤ζΤΖ÷–≥ι»Γ![]() ΦΰΘ§≤βΝΩ’β–©≤ζΤΖΒΡ“Μœν÷ ΝΩ÷Η±ξ÷ΒΘ§”…≤βΝΩΫαΙϊΒΟ»γΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘΚ
ΦΰΘ§≤βΝΩ’β–©≤ζΤΖΒΡ“Μœν÷ ΝΩ÷Η±ξ÷ΒΘ§”…≤βΝΩΫαΙϊΒΟ»γΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘΚ
Θ®1Θ©«σ’β![]() Φΰ≤ζΤΖ÷ ΝΩ÷Η±ξ÷ΒΒΡ―υ±ΨΤΫΨυ ΐ
Φΰ≤ζΤΖ÷ ΝΩ÷Η±ξ÷ΒΒΡ―υ±ΨΤΫΨυ ΐ![]() ΚΆ―υ±ΨΖΫ≤ν
ΚΆ―υ±ΨΖΫ≤ν![]() Θ®Ά§“ΜΉι÷–ΒΡ ΐΨί”ΟΗΟΉι«χΦδΒΡ÷–Βψ÷ΒΉς¥ζ±μΘ©ΘΜ
Θ®Ά§“ΜΉι÷–ΒΡ ΐΨί”ΟΗΟΉι«χΦδΒΡ÷–Βψ÷ΒΉς¥ζ±μΘ©ΘΜ
Θ®2Θ©”…÷±ΖΫΆΦΩ…“‘»œΈΣΘ§’β÷÷≤ζΤΖΒΡ÷ ΝΩ÷Η±ξ÷Β![]() Ζΰ¥”’ΐΧ§Ζ÷≤Φ
Ζΰ¥”’ΐΧ§Ζ÷≤Φ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() ΫϋΥΤΈΣ―υ±ΨΤΫΨυ ΐ
ΫϋΥΤΈΣ―υ±ΨΤΫΨυ ΐ![]() Θ§
Θ§![]() ΫϋΥΤΈΣ―υ±ΨΖΫ≤ν
ΫϋΥΤΈΣ―υ±ΨΖΫ≤ν![]() .
.
ΔΌάϊ”ΟΗΟ’ΐΧ§Ζ÷≤ΦΘ§«σ![]() ΘΜ
ΘΜ
ΔΎΡ≥”ΟΜߥ”ΗΟΤσ“ΒΙΚ¬ρΝΥ![]() Φΰ’β÷÷≤ζΤΖΘ§Φ«
Φΰ’β÷÷≤ζΤΖΘ§Φ«![]() ±μ Ψ’β
±μ Ψ’β![]() Φΰ≤ζΤΖ÷–÷ ΝΩ÷Η±ξ÷ΒΈΜ”Ύ«χΦδ
Φΰ≤ζΤΖ÷–÷ ΝΩ÷Η±ξ÷ΒΈΜ”Ύ«χΦδ![]() ΒΡ≤ζΤΖΦΰ ΐ.άϊ”ΟΔΌΒΡΫαΙϊΘ§«σ
ΒΡ≤ζΤΖΦΰ ΐ.άϊ”ΟΔΌΒΡΫαΙϊΘ§«σ![]() .
.
ΗΫΘΚ![]() .»τ
.»τ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§![]() .
.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§
Θ§![]() ΘΜΘ®2Θ©68.26
ΘΜΘ®2Θ©68.26
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®ΔώΘ©‘Υ”Οάκ…Δ–ΆΥφΜζ±δΝΩΒΡΤΎΆϊΚΆΖΫ≤νΙΪ ΫΘ§Φ¥Ω…«σ≥ωΘΜΘ®ΔρΘ©Θ®iΘ©”…Θ®ΔώΘ©÷ΣZΓΪNΘ®200Θ§150Θ©Θ§¥”Εχ«σ≥ωPΘ®187Θ°8ΘΦZΘΦ212Θ°2Θ©Θ§ΉΔ“β‘Υ”ΟΥυΗχ ΐΨίΘΜΘ®iiΘ©”…Θ®iΘ©÷ΣXΓΪBΘ®100Θ§0Θ°6826Θ©Θ§‘Υ”ΟEX=npΦ¥Ω…«σΒΟ
‘ΧβΫβΈωΘΚΘ®1Θ©≥ι»Γ≤ζΤΖΒΡ÷ ΝΩ÷Η±ξ÷ΒΒΡ―υ±ΨΤΫΨυ ΐ![]() ΚΆ―υ±ΨΖΫ≤νs2Ζ÷±πΈΣ
ΚΆ―υ±ΨΖΫ≤νs2Ζ÷±πΈΣ
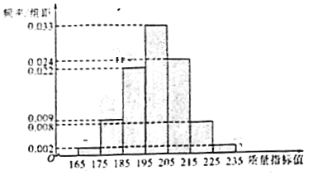
![]() ΘΫ170ΓΝ0Θ°02ΘΪ180ΓΝ0Θ°09ΘΪ190ΓΝ0Θ°22ΘΪ200ΓΝ0Θ°33ΘΪ210ΓΝ0Θ°24ΘΪ220ΓΝ0Θ°08ΘΪ230ΓΝ0Θ°02ΘΫ200Θ°
ΘΫ170ΓΝ0Θ°02ΘΪ180ΓΝ0Θ°09ΘΪ190ΓΝ0Θ°22ΘΪ200ΓΝ0Θ°33ΘΪ210ΓΝ0Θ°24ΘΪ220ΓΝ0Θ°08ΘΪ230ΓΝ0Θ°02ΘΫ200Θ°
s2ΘΫΘ®Θ≠30Θ©2ΓΝ0Θ°02ΘΪΘ®Θ≠20Θ©2ΓΝ0Θ°09ΘΪΘ®Θ≠10Θ©2ΓΝ0Θ°22ΘΪ0ΓΝ0Θ°33ΘΪ102ΓΝ0Θ°24ΘΪ202ΓΝ0Θ°08ΘΪ302ΓΝ0Θ°02ΘΫ150Θ°Γ≠6Ζ÷
Θ®2Θ©Θ®iΘ©”…Θ®1Θ©÷ΣΘ§ZΓΪNΘ®200Θ§150Θ©Θ§
¥”ΕχPΘ®187Θ°8ΘΦZΘΦ212Θ°2Θ©ΘΫPΘ®200Θ≠12Θ°2ΘΦZΘΦ200ΘΪ12Θ°2Θ©ΘΫ0Θ°682 6Θ°
Θ®iiΘ©”…Θ®iΘ©÷ΣΘ§“ΜΦΰ≤ζΤΖΒΡ÷ ΝΩ÷Η±ξ÷ΒΈΜ”Ύ«χΦδΘ®187Θ°8Θ§212Θ°2Θ©ΒΡΗ≈¬ ΈΣ0Θ°682 6Θ§
“άΧβ“β÷ΣXΓΪBΘ®100Θ§0Θ°682 6Θ©Θ§
Υυ“‘EXΘΫ100ΓΝ0Θ°682 6ΘΫ68Θ°26Θ°

 Οϊ–ΘΆ®––÷Λ”––ßΉς“ΒœΒΝ–¥πΑΗ
Οϊ–ΘΆ®––÷Λ”––ßΉς“ΒœΒΝ–¥πΑΗ





