题目内容
15.关于x的不等式${2^{{x^2}+2b}}<{2^{-ax}}$有唯一整数解x=1,则$\frac{b-2}{a-1}$的取值范围是($\frac{1}{4}$,1).分析 将不等式进行等价转化,利用根与系数之间的关系建立不等式组,利用线性规划的知识进行求解即可.
解答 解:∵${2^{{x^2}+2b}}<{2^{-ax}}$?x2+ax+2b<0,
∴依题意方程x2+ax+2b=0只有唯一的整数解x=1,
∴方程x2+ax+2b=0一根在[0,1)内,另一根在(1,2]内,
即函数f(x)=x2+ax+2b的图象与x轴在[0,1)和(1,2]内各有一个交点.
∴$\left\{{\begin{array}{l}{f(0)≥0}\\{f(1)<0}\\{f(2)≥0}\end{array}}\right.⇒\left\{{\begin{array}{l}{b≥0}\\{a+2b+1<0}\\{a+b+2≥0}\end{array}}\right.$,作出可行域,如图所示: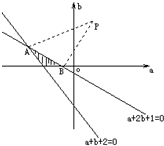
∵$\frac{b-2}{a-1}$为可行域内的点(a,b)与定点P(1,2)的连线的斜率,
由图可知,kPA<$\frac{b-2}{a-1}$<kPB,其中点A(-3,1),B(-1,0),
∴kPA=$\frac{1}{4}$,kPB=1,故$\frac{b-2}{a-1}$的取值范围是($\frac{1}{4}$,1).
故答案为:($\frac{1}{4}$,1).
点评 本题主要考查线性规划的应用,根据不等式的性质结合一元二次函数根与系数之间的关系进行转化是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知f(x)=cos(ωx+$\frac{π}{6}$)(ω>0)的图象与直线y=1的两个交点的最短距离是π,要得到y=f(x)的图象,只需要把y=sinωx的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
20.已知(1+i)•z=2i,那么复数z对应的点位于复平面内的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.设全集U={x∈R|x≥0},函数f(x)=$\sqrt{1-lgx}$的定义域为M,则∁UM为( )
| A. | (10,+∞)∪{0} | B. | (10,+∞) | C. | (0,10) | D. | (0,10] |