题目内容
10.过抛物线C:x2=4y对称轴上任一点P(0,m)(m>0)作直线l与抛物线交于A,B两点,点Q是点P关于原点的对称点.(1)当直线l方程为x-2y+12=0时,过A,B两点的圆M与抛物线在点A处有共同的切线,求圆M的方程
(2)设$\overrightarrow{AP}$=λ$\overrightarrow{PB}$,证明:$\overrightarrow{QP}$⊥($\overrightarrow{QA}$-λ$\overrightarrow{QB}$)
分析 (1)由$\left\{\begin{array}{l}{x-2y+12=0}\\{{x}^{2}=4y}\end{array}\right.$得点A、B的坐标分别是(6,9)、(-4,4).求出AB的垂直平分线方程,抛物线在点A处的切线斜率为3.利用待定系数法,求出圆M的方程;
(2)可设直线AB的方程为y=kx+m,代入抛物线方程x2=4y得x2-4kx-4m=0.设A、B两点的坐标分别是(x1,y1)、(x2,y2),x1x2=-4m.由$\overrightarrow{AP}$=λ$\overrightarrow{PB}$,得λ=-$\frac{{x}_{1}}{{x}_{2}}$.由此可以推出$\overrightarrow{QP}$⊥($\overrightarrow{QA}$-λ$\overrightarrow{QB}$).
解答 (1)解:由$\left\{\begin{array}{l}{x-2y+12=0}\\{{x}^{2}=4y}\end{array}\right.$得点A、B的坐标分别是(6,9)、(-4,4),
则AB的中点为(1,$\frac{13}{2}$),斜率为k=$\frac{9-4}{6-(-4)}$=$\frac{1}{2}$,
故AB的垂直平分线方程为4x+2y-17=0.
由x2=4y得y=$\frac{1}{4}{x}^{2}$,y′=$\frac{1}{2}x$,所以抛物线在点A处的切线斜率为3
设圆M的方程为(x-a)2+(y-b)2=r2,则$\left\{\begin{array}{l}{\frac{b-9}{a-6}=-\frac{1}{3}}\\{a+b-14=0}\end{array}\right.$
解得a=-$\frac{3}{2}$,b=$\frac{23}{2}$,r2=$\frac{125}{2}$
所以圆M的方程为(x+$\frac{3}{2}$)2+(y-$\frac{23}{2}$)2=$\frac{125}{2}$;
(2)证明:设AB方程为y=kx+m,A、B两点的坐标分别是(x1,y1)、(x2,y2),
代入抛物线方程x2=4y得x2-4kx-4m=0,x1+x2=-4k,x1x2=-4m
由$\overrightarrow{AP}$=λ$\overrightarrow{PB}$,得λ=-$\frac{{x}_{1}}{{x}_{2}}$,又点Q(0,2m),从而$\overrightarrow{QP}$=(0,2m)
$\overrightarrow{QA}$-λ$\overrightarrow{QB}$=(x1-λx2,y1-λy2+(1-λ)m),
所以$\overrightarrow{QP}$•($\overrightarrow{QA}$-λ$\overrightarrow{QB}$)=2m[y1-λy2+(1-λ)m]=2m(x1+x2)•$\frac{{x}_{1}{x}_{2}+4m}{4{x}_{2}}$=0
所以$\overrightarrow{QP}$⊥($\overrightarrow{QA}$-λ$\overrightarrow{QB}$).
点评 本题考查直线和圆锥曲线的位置关系,考查圆的方程,考查向量知识,考查学生分析解决问题的能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{4}{41}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{25}$ | D. | $\frac{4\sqrt{41}}{41}$ |
| A. | -8 | B. | 8 | C. | 5 | D. | 15 |
 过圆外一点P作圆的切线PA(A为切点),再作割线PBC与圆交于B,C.若PA=6,AC=8,BC=9,则AB=4.
过圆外一点P作圆的切线PA(A为切点),再作割线PBC与圆交于B,C.若PA=6,AC=8,BC=9,则AB=4.
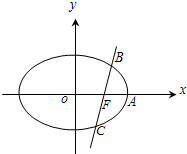 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),且过点(-1,$\frac{3}{2}$),右顶点为A,经过点F的动直线l与椭圆交于B,C两点.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),且过点(-1,$\frac{3}{2}$),右顶点为A,经过点F的动直线l与椭圆交于B,C两点.