Question

【题目】已知函数
（1）当a=0时，求f（x）的极值．
（2）当a≠0时，若f（x）是减函数，求a的取值范围；

Answer 1

【答案】
（1）解：∵

当a=0时，f（x）=2x﹣lnx，则

∴x，f'（x），f（x）的变化情况如下表

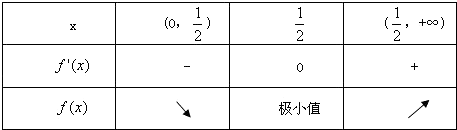
∴当 时，f（x）的极小值为1+ln2，函数无极大值

（2）解：由已知，得 ，且x＞0，则

∵函数f（x）是减函数

∴f'（x）≤0对x＞0恒成立，即不等式 为 对恒成立

由二次函数的性质可得

解得a≤﹣1，即a的取值范围是（﹣∞，﹣1]

另解： 对x＞0恒成立，即 对x＞0恒成立，即

【解析】求函数的定义域（0，+∞）（1）把a=0代入求导，研究函数的单调区间，根据单调性求函数的极值．（2）由题意可得f′（x）≤0在（0，+∞）恒成立，转化为求函数f′（x）在（0，+∞）的最大值小于（等于）0，进而求解，也可利用二次函数的图象及根的分布问题求解．
【考点精析】根据题目的已知条件，利用函数的极值与导数的相关知识可以得到问题的答案，需要掌握求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值．