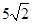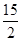题目内容
已知函数 f(x)的定义域为 ,其导函数f'(x)的图象如图所示,则对于任意
,其导函数f'(x)的图象如图所示,则对于任意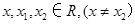 ,下列结论正确的是( )
,下列结论正确的是( )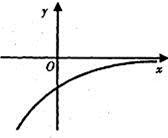
①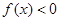 恒成立;
恒成立;
②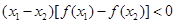 ;
;
③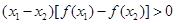 ;
;
④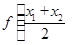 >
> 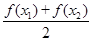 ;
;
⑤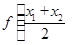 <
< 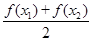 .
.
| A.①③ | B.①③④ | C.②④ | D.②⑤ |
D
解析试题分析:由导函数的图象可知,导函数f′(x)的图象在x轴下方,即f′(x)<0,故原函数为减函数,并且是递减的速度是先快后慢,所以函数的图像称下凸形状。
f(x)<0恒成立,没有依据,故①不正确;
②表示(x1-x2)与[f(x1)-f(x2)]异号,即f(x)为减函数.故②正确;
③表示(x1-x2)与[f(x1)-f(x2)]同号,即f(x)为增函数.故③不正确,
④⑤左边边的式子意义为x1,x2中点对应的函数值, 右边式子代表的是函数值得平均值,因为图像为下凸的,显然有左边小于右边,故④不正确,⑤正确,综上,正确的结论为②⑤.故选D.
考点:利用导数研究函数的单调性;导数的几何意义。
点评:本题为导函数的应用,由导函数的图象推出原函数应具备的性质,利用数形结合是解决问题的关键,属基础题.

练习册系列答案
相关题目
函数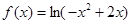 的单调递增区间是( )
的单调递增区间是( )
A.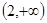 | B.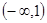 | C.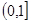 | D.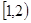 |
已知函数 是定义域为R的偶函数,且
是定义域为R的偶函数,且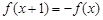 ,若
,若 在
在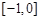 上是增函数,那么
上是增函数,那么 在
在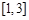 上是
上是
| A.增函数 | B.减函数 | C.先增后减的函数 | D.先减后增的函数 |
定义在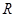 上的函数
上的函数 既是偶函数又是周期函数,若
既是偶函数又是周期函数,若 的最小正周期是
的最小正周期是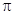 ,且当
,且当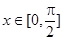 时,
时,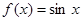 ,则
,则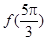 的值为( )
的值为( )
A.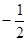 | B.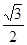 | C. | D.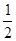 |
已知函数 ( )
( )
A. | B. | C. | D. |
在函数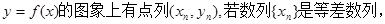 数列{
数列{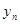 }是等比数列,则函数
}是等比数列,则函数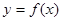 的解析式可能为( )
的解析式可能为( )
A.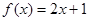 | B.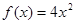 |
C.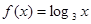 | D.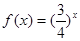 |
函数 的最大值是( )
的最大值是( )
A. | B. | C. | D. |
已知函数 是奇函数,当
是奇函数,当 时,
时, ,则
,则 的值为
的值为
A. | B. | C. | D. |
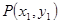 、
、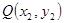 之间的“理想距离”为:
之间的“理想距离”为: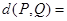
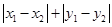 ;若
;若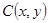 到点
到点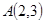 、
、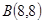 的“理想距离”相等,其中实数
的“理想距离”相等,其中实数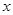 、
、 满足
满足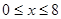 、
、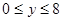 ,则所有满足条件的点
,则所有满足条件的点 的轨迹的长度之和是
的轨迹的长度之和是