题目内容
函数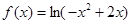 的单调递增区间是( )
的单调递增区间是( )
A.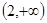 | B.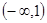 | C.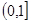 | D.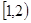 |
C
解析试题分析:令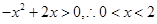 ,而
,而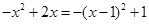 ,以
,以 为对称轴,根据复合
为对称轴,根据复合
函数的单调性可知,函数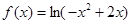 的单调递增区间是
的单调递增区间是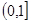 .
.
考点:本小题主要考查复合函数的单调性.
点评:复合函数的单调性符合“同增异减”的原则,但是求解单调区间之前,要先考查函数的单调性.

练习册系列答案
相关题目
下列函数中,满足 的是( )
的是( )
A. | B.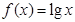 | C. | D. |
函数 的定义域为开区间
的定义域为开区间 ,导函数
,导函数 在
在 内的图象如图所示,则函数
内的图象如图所示,则函数 在开区间
在开区间 内有极小值点( )
内有极小值点( )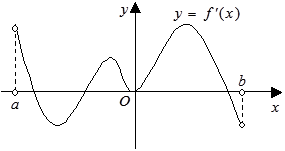
| A.4个 | B. 个 个 | C. 个 个 | D.1个 |
已知单位向量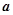 、
、 ,满足
,满足 ,则函数
,则函数 (
( )
)
| A.既是奇函数又是偶函数 | B.既不是奇函数也不是偶函数 |
| C.是偶函数 | D.是奇函数 |
设奇函数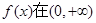 上为减函数,且
上为减函数,且 ,则不等式
,则不等式 的解集为( )
的解集为( )
A. | B. |
C. | D. |
已知定义域为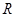 的函数
的函数 满足
满足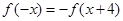 ,则
,则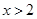 时,
时, 单调递增,若
单调递增,若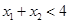 ,且
,且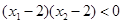 ,则
,则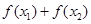 与0的大小关系是( )
与0的大小关系是( )
A.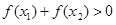 | B.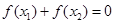 |
C. | D.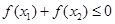 |
已知函数 f(x)的定义域为 ,其导函数f'(x)的图象如图所示,则对于任意
,其导函数f'(x)的图象如图所示,则对于任意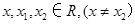 ,下列结论正确的是( )
,下列结论正确的是( )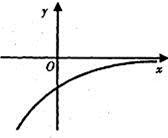
①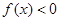 恒成立;
恒成立;
②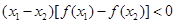 ;
;
③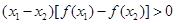 ;
;
④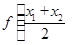 >
> 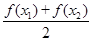 ;
;
⑤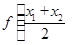 <
< 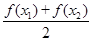 .
.
| A.①③ | B.①③④ | C.②④ | D.②⑤ |
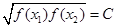 ,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为
,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为 B.2 C.4 D. 2
B.2 C.4 D. 2 的图象的是
的图象的是