Question

【题目】如图，在四面体ABOC中，OC⊥OA，OC⊥OB，∠AOB=120°，且OA=OB=OC=1
（Ⅰ）设为P为AC的中点，Q为AB上一点，使PQ⊥OA，并计算 的值；
（Ⅱ）求二面角O﹣AC﹣B的平面角的余弦值．

Answer 1

【答案】解：法一：
（Ⅰ）在平面OAB内作ON⊥OA交AB于N，连接NC．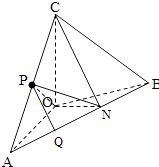

又OA⊥OC，∴OA⊥平面ONC
∵NC平面ONC，
∴OA⊥NC．
取Q为AN的中点，则PQ∥NC．
∴PQ⊥OA
在等腰△AOB中，∠AOB=120°，
∴∠OAB=∠OBA=30°
在Rt△AON中，∠OAN=30°，
∴
在△ONB中，∠NOB=120°﹣90°=30°=∠NBO，
∴NB=ON=AQ．
∴
（Ⅱ）连接PN，PO，
由OC⊥OA，OC⊥OB知：OC⊥平面OAB．
又ON平面OAB，
∴OC⊥ON
又由ON⊥OA，ON⊥平面AOC．
∴OP是NP在平面AOC内的射影．
在等腰Rt△COA中，P为AC的中点，
∴AC⊥OP
根据三垂线定理，知：
∴AC⊥NP
∴∠OPN为二面角O﹣AC﹣B的平面角
在等腰Rt△COA中，OC=OA=1，∴
在Rt△AON中， ，
∴在Rt△PON中， ．
∴
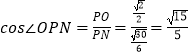
解法二：
（I）取O为坐标原点，分别以OA，OC所在的直线为x轴，z轴，
建立空间直角坐标系O﹣xyz（如图所示）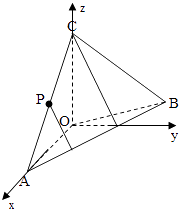

则
∵P为AC中点，∴
设 ，∵ ．
∴ ，
∴ ．
∵ ，
∴ 即 ， ．
所以存在点 使得PQ⊥OA且 ．
（Ⅱ）记平面ABC的法向量为 =（n1 ， n2 ， n3），则由 ， ，
得 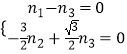，故可取
又平面OAC的法向量为 =（0，1，0）．
∴cos＜ ， ＞= ．
两面角O﹣AC﹣B的平面角是锐角，记为θ，则
【解析】解法一：（1）要计算 的值，我们可在平面OAB内作ON⊥OA交AB于N，连接NC．则根据已知条件结合平面几何中三角形的性质我们易得NB=ON=AQ，则易求出 的值．（2）要求二面角O﹣AC﹣B的平面角的余弦值，我们可连接PN，PO，根据三垂线定理，易得∠OPN为二面角O﹣AC﹣B的平面角，然后解三角形OPN得到二面角O﹣AC﹣B的平面角的余弦值．
解法二：取O为坐标原点，分别以OA，OC所在的直线为x轴，z轴，建立空间直角坐标系O﹣xyz，我们易根据已知给出四面体中各点的坐标，利用向量法进行求解，（1）由A、Q、B三点共线，我们可设 ，然后根据已知条件，构造关于λ的方程，解方程即可得到λ的值，即 的值；（2）要求二面角O﹣AC﹣B的平面角的余弦值，我们可以分别求出平面OAC及平面ABC的法向量，然后根据求二面角O﹣AC﹣B的平面角的余弦值等于两个法向量夹角余弦的绝对值进行求解．
【考点精析】根据题目的已知条件，利用平面与平面之间的位置关系的相关知识可以得到问题的答案，需要掌握两个平面平行没有交点；两个平面相交有一条公共直线．