题目内容
【题目】在平面直角坐标系xOy中,已知抛物线C:x2=4y,点P是C的准线l上的动点,过点P作C的两条切线,切点分别为A,B,则△AOB面积的最小值为( )
A.![]()
B.2
C.2 ![]()
D.4
【答案】B
【解析】解:如图所示:抛物线C:x2=4y,准线l的方程y=﹣1,设P(x0 , ﹣1),A(x1 , y1),B(x2 , y2), 由y= ![]() x2 , 求导y′=
x2 , 求导y′= ![]() x,
x,
切线PA的方程为y﹣x1= ![]() x1(x﹣x1),即y=
x1(x﹣x1),即y= ![]() x1x﹣y1 ,
x1x﹣y1 ,
又切线PA过点P(x0 , ﹣1),﹣1= ![]() x1x0﹣y1 ,
x1x0﹣y1 ,
整理得:x1x0﹣2y1+2=0,
同理切线PB的方程x2x0﹣2y2+2=0,
∴直线AB的方程为xx0﹣2y+2=0,
直线AB过定点F(0,1),
∴△AOB面积,S= ![]() 丨OF丨丨x1﹣x2丨=
丨OF丨丨x1﹣x2丨= ![]() 丨x1﹣x2丨≥
丨x1﹣x2丨≥ ![]() ×4=2,
×4=2,
∴当且仅当直线AB⊥y轴时取等号,
∴△AOB面积的最小值2,
故选B.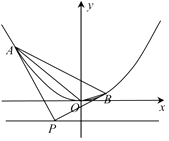

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
【题目】爱心超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完![]() 根据往年销售经验,每天需求量与当天最高气温
根据往年销售经验,每天需求量与当天最高气温![]() 单位:
单位:![]() 有关
有关![]() 如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶
,需求量为300瓶;如果最高气温低于20,需求量为200瓶![]() 为了确定六月份的订购计划,统计了前三年六月份每天的最高气温数据,得到下面的频数分布表:
为了确定六月份的订购计划,统计了前三年六月份每天的最高气温数据,得到下面的频数分布表:
最高气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(1)求六月份这种酸奶一天的需求量不超过300瓶的频率;
(2)当六月份有一天这种酸奶的进货量为450瓶时,求这一天销售这种酸奶的平均利润(单位:元)
