题目内容
7.已知椭圆C1的方程为:$\frac{x^2}{169}+\frac{y^2}{144}=1$,若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为( )| A. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{169}-\frac{y^2}{144}=1$ | C. | $\frac{x^2}{169}-\frac{y^2}{25}=1$ | D. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ |
分析 通过椭圆方程即得双曲线C2的焦点坐标,利用定义可得结论.
解答 解:由题易知曲线C2即为双曲线,设其方程为:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,
∵椭圆C1的方程为:$\frac{x^2}{169}+\frac{y^2}{144}=1$,
∴椭圆C1的焦点坐标分别为:(5,0)、(-5,0),
∴双曲线C2是以(5,0)、(-5,0)为焦点、2a=8的双曲线,
则a=4,c=5,b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
即双曲线C2的方程为:$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1,
故选:D.
点评 本题考查椭圆、双曲线的简单性质,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
2.椭圆的一焦点与两顶点为等边三角形的三个顶点,则椭圆的长轴长是短轴长的( )
| A. | $\sqrt{3}$倍 | B. | 2倍 | C. | $\sqrt{2}$倍 | D. | $\frac{3}{2}$倍 |
19.已知周长为16的△ABC的两顶点与椭圆M的两个焦点重合,另一个顶点恰好在椭圆M上,则下列椭圆中符合椭圆M条件的是( )
| A. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | B. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{9}$+$\frac{{x}^{2}}{4}$=1 |
17.若直线ax-y+1=0与直线2x+y+2=0平行,则a的值为( )
| A. | -2 | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
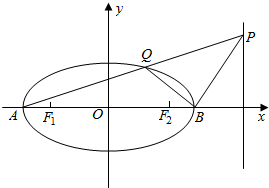 椭圆E:$\frac{{x}^{2}}{4}$+y2=1的左、右焦点分别为F1,F2,左、右顶点分别为A,B.
椭圆E:$\frac{{x}^{2}}{4}$+y2=1的左、右焦点分别为F1,F2,左、右顶点分别为A,B.