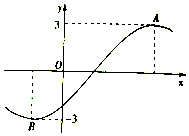题目内容
【题目】设函数f（x）=lnx+ 
，m∈R，若对任意b＞a＞0， 
＜1恒成立，则m的取值范围为 ．
【答案】[ 
，+∞）
【解析】（Ⅲ）对任意b＞a＞0， 
＜1恒成立，
等价于f（b）﹣b＜f（a）﹣a恒成立；
设h（x）=f（x）﹣x=lnx+ 
﹣x（x＞0），
则h（b）＜h（a）．
∴h（x）在（0，+∞）上单调递减；
∵h′（x）= 
﹣ 
﹣1≤0在（0，+∞）上恒成立，
∴m≥﹣x2+x=﹣（x﹣ 
）2+ （x＞0），
∴m≥ ；
对于m= ，h′（x）=0仅在x= 时成立；
∴m的取值范围是[ ，+∞）．
【考点精析】利用函数的最大(小)值与导数对题目进行判断即可得到答案，需要熟知求函数
在
上的最大值与最小值的步骤：（1）求函数在
内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值．
练习册系列答案
智慧小复习系列答案
相关题目
【题目】已知函数f（x）的定义域为[﹣1，5]，部分对应值如表，
x | ﹣1 | 0 | 4 |
f（x） | 1 | 2 | 2 |
f（x）的导函数y=f′（x）的图象（该图象关于（2，0）中心对称） 如图所示．
下列关于f（x）的命题：
①函数f（x）的极大值点为 0与4；
②函数f（x）在[0，2]上是减函数；
③函数y=f（x）﹣a零点的个数可能为0、1、2、3、4个；
④如果当时x∈[﹣1，t]，f（x）的最大值是2，那么t的最大值为5；．
⑤函数f（x）的图象在a=1是上凸的
其中一定正确命题的序号是 ． 
