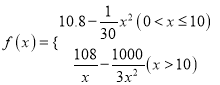题目内容
【题目】已知数列 
Sn为其前n项和．计算得 
观察上述结果，推测出计算Sn的公式，并用数学归纳法加以证明．
【答案】解：观察分析题设条件可知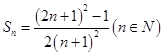 
证明如下：（i）当n=1时， 
，等式成立．
（ii）设当n=k时等式成立，即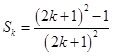 
则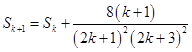 
= 
= 
= 
= 
= 
= 
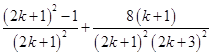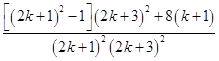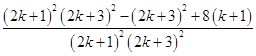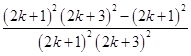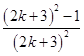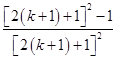
由此可知，当n=k+1时等式也成立．根据（1）（2）可知，等式对任何n∈N都成立
【解析】观察分析题设条件可知 
．然后再用数学归纳法进行证明．
【考点精析】根据题目的已知条件，利用数列的通项公式和数学归纳法的定义的相关知识可以得到问题的答案，需要掌握如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式；数学归纳法是证明关于正整数n的命题的一种方法．
练习册系列答案
相关题目
【题目】已知f（x+y）=f（x）+f（y）且f（1）=2，则f（1）+f（2）+…+f（n）不能等于（ ）
A.f（1）+2f（1）+…+nf（1）
B.f（ 
）
C.n（n+1）
D.n（n+1）f（1）
【题目】如表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x（吨）与相应的生产能耗y（吨）的几组对应数据，根据表提供的数据，求出y关于x的线性回归方程为 
=0.7x+0.35，则下列结论错误的是（ ）
x | 3 | 4 | 5 | 6 |
y | 2.5 | t | 4 | 4.5 |
A.产品的生产能耗与产量呈正相关
B.t的取值必定是3.15
C.回归直线一定过点（4，5，3，5）
D.A产品每多生产1吨，则相应的生产能耗约增加0.7吨
