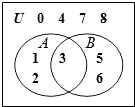
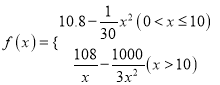题目内容
【题目】[ 
]表示不超过 的最大整数．若 S1=[ 
]+[ 
]+[ 
]=3，
S2=[ 
]+[ 
]+[ 
]+[ 
]+[ 
]=10，
S3=[ 
]+[ 
]+[ 
]+[ 
]+[ 
]+[ 
]+[ 
]=21，
…，
则Sn=（ ）
A.n（n+2）
B.n（n+3）
C.（n+1）2﹣1
D.n（2n+1）
【答案】D
【解析】解：第一个等式，起始数为：1，项数为：3=4﹣1=22﹣12 ， S1=1×3； 第二个等式，起始数为：2，项数为：5=9﹣4=32﹣22 ， S2=2×5；
第三个等式，起始数为：3，项数为：7=16﹣9═42﹣32 ， S3=3×7；
…
第n个等式，起始数为：n，项数为：（n+1）2﹣n2=2n+1，Sn=n（2n+1），（n∈N*）．
故选：D．
【考点精析】根据题目的已知条件，利用归纳推理的相关知识可以得到问题的答案，需要掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理．
【题目】如表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x（吨）与相应的生产能耗y（吨）的几组对应数据，根据表提供的数据，求出y关于x的线性回归方程为 
=0.7x+0.35，则下列结论错误的是（ ）
x | 3 | 4 | 5 | 6 |
y | 2.5 | t | 4 | 4.5 |
A.产品的生产能耗与产量呈正相关
B.t的取值必定是3.15
C.回归直线一定过点（4，5，3，5）
D.A产品每多生产1吨，则相应的生产能耗约增加0.7吨
【题目】某市政府为了确定一个较为合理的居民用电标准，必须先了解全市居民日常用电量的分布情况．现采用抽样调查的方式，获得了n位居民在2012年的月均用电量（单位：度）数据，样本统计结果如下图表：
分 组 | 频 数 | 频 率 |
[0，10） | 0.05 | |
[10，20） | 0.10 | |
[20，30） | 30 | |
[30，40） | 0.25 | |
[40，50） | 0.15 | |
[50，60] | 15 | |
合 计 | n | 1 |
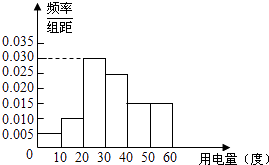
（1）求月均用电量的中位数与平均数估计值；
（2）如果用分层抽样的方法从这n位居民中抽取8位居民，再从这8位居民中选2位居民，那么至少有1位居民月均用电量在30至40度的概率是多少？
（3）用样本估计总体，把频率视为概率，从这个城市随机抽取3位居民（看作有放回的抽样），求月均用电量在30至40度的居民数X的分布列．
