题目内容
【题目】解答题
(Ⅰ)已知函数f(x)=|x+1|+|x﹣a|(a>0),若不等式f(x)≥5的解集为{x|x≤﹣2或x≥3},求a的值;
(Ⅱ) 已知实数a,b,c∈R+ , 且a+b+c=m,求证: ![]() +
+ ![]() +
+ ![]() ≥
≥ ![]() .
.
【答案】解:(Ⅰ) 因为a>0,所以 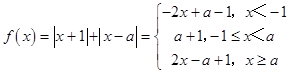 , 又因为不等式f(x)≥5的解集为{x|x≤﹣2或x≥3},就是x=﹣2或x=3时,f(x)=5,解得a=2.(5分)
, 又因为不等式f(x)≥5的解集为{x|x≤﹣2或x≥3},就是x=﹣2或x=3时,f(x)=5,解得a=2.(5分)
(Ⅱ)证明: 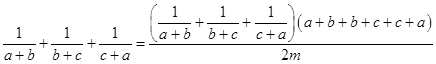
= 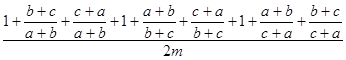
= 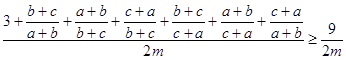
【解析】(Ⅰ)化简函数f(x)=|x+1|+|x﹣a|(a>0)为分段函数,然后通过不等式f(x)≥5的解集为{x|x≤﹣2或x≥3},求a的值;(Ⅱ)利用“1”的代换,利用基本不等式转化证明即可.
【考点精析】解答此题的关键在于理解不等式的证明的相关知识,掌握不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等.

【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
.
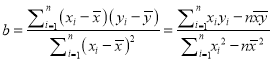 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2) ![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?
【题目】已知二次函数![]() 的最小值为3,且
的最小值为3,且![]() .
.
求函数![]() 的解析式;
的解析式;
(2)若偶函数![]() (其中
(其中![]() ),那么,
),那么, ![]() 在区间
在区间![]() 上是否存在零点?请说明理由.
上是否存在零点?请说明理由.
【答案】(1)![]() (2)存在零点
(2)存在零点
【解析】试题分析:(1)待定系数法,己知函数类型为二次函数,又知f(-1)=f(3),所以对称轴是x=1,且函数最小值f(1)=3,所设函数![]() ,且
,且![]() ,代入f(-1)=11,可解a。
,代入f(-1)=11,可解a。
(2)由题意可得![]() ,代入
,代入![]() ,由
,由![]() 和根的存在性定理,
和根的存在性定理, ![]() 在区间(1,2)上存在零点。
在区间(1,2)上存在零点。
试题解析:(1)因为![]() 是二次函数,且
是二次函数,且![]()
所以二次函数图像的对称轴为![]() .
.
又![]() 的最小值为3,所以可设
的最小值为3,所以可设![]() ,且
,且![]()
由![]() ,得
,得![]()
所以![]()
(2)由(1)可得![]() ,
,
因为![]() ,
,
![]()
所以![]() 在区间(1,2)上存在零点.
在区间(1,2)上存在零点.
【点睛】
(1)对于求己知类型函数的的解析式,常用待定系数法,由于二次函数的表达式形式比较多,有一般式,两点式,顶点式,由本题所给条件知道对称轴与顶点坐标,所以设顶点式。
(2)对于判定函数在否存在零点问题,一般解决此类问题的三步曲是:①先通过观察函数图象再估算出根所在的区间;②根据方程根的存在性定理证明根是存在的;③最后根据函数的性质证明根是唯一的.本题给了区间,可直接用根的存在性定理。
【题型】解答题
【结束】
20
【题目】《中华人民共和国个人所得税》规定,公民月工资、薪金所得不超过3500元的部分不纳税,超过3500元的部分为全月税所得额,此项税款按下表分段累计计算:
全月应纳税所得额 | 税率 |
不超过1500元的部分 |
|
超过1500元至4500元的部分 |
|
超过4500元至9000元的部分 |
|
(1)已知张先生的月工资,薪金所得为10000元,问他当月应缴纳多少个人所得税?
(2)设王先生的月工资,薪金所得为![]() ,当月应缴纳个人所得税为
,当月应缴纳个人所得税为![]() 元,写出
元,写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)已知王先生一月份应缴纳个人所得税为303元,那么他当月的工资、薪金所得为多少?