题目内容
选修4-1:几何证明选讲
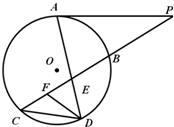
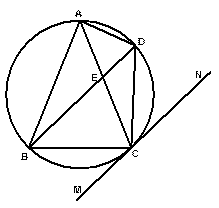
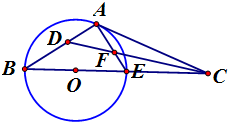
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且DE2=EF•EC.
(1)求证:CE•EB=EF•EP;
(2)若CE:BE=3:2,DE=3,EF=2,求PA的长.
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且DE2=EF•EC.
(1)求证:CE•EB=EF•EP;
(2)若CE:BE=3:2,DE=3,EF=2,求PA的长.

(I)证明:∵DE2=EF•EC,∠DEF公用,
∴△DEF∽△CED,
∴∠EDF=∠C.
又∵弦CD∥AP,∴∠P=∠C,
∴∠EDF=∠P,∠DEF=∠PEA
∴△EDF∽△EPA.
∴
=
,∴EA•ED=EF•EP.
又∵EA•ED=CE•EB,
∴CE•EB=EF•EP;
(II)∵DE2=EF•EC,DE=3,EF=2.
∴32=2EC,∴CE=
.
∵CE:BE=3:2,∴BE=3.
由(I)可知:CE•EB=EF•EP,∴
×3=2EP,解得EP=
,
∴BP=EP-EB=
-3=
.
∵PA是⊙O的切线,∴PA2=PB•PC,
∴PA2=
×(
+
),解得PA=
.
∴△DEF∽△CED,
∴∠EDF=∠C.
又∵弦CD∥AP,∴∠P=∠C,
∴∠EDF=∠P,∠DEF=∠PEA
∴△EDF∽△EPA.
∴
| EA |
| EF |
| EP |
| ED |
又∵EA•ED=CE•EB,
∴CE•EB=EF•EP;
(II)∵DE2=EF•EC,DE=3,EF=2.
∴32=2EC,∴CE=
| 9 |
| 2 |
∵CE:BE=3:2,∴BE=3.
由(I)可知:CE•EB=EF•EP,∴
| 9 |
| 2 |
| 27 |
| 4 |
∴BP=EP-EB=
| 27 |
| 4 |
| 15 |
| 4 |
∵PA是⊙O的切线,∴PA2=PB•PC,
∴PA2=
| 15 |
| 4 |
| 27 |
| 4 |
| 9 |
| 2 |
15
| ||
| 4 |

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
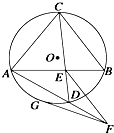
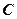 是内接于⊙O,
是内接于⊙O,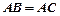 ,直线
,直线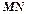 切⊙O于点
切⊙O于点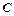 ,弦
,弦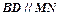 ,
,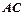 与
与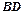 相交于点
相交于点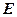 .
.
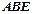 ≌Δ
≌Δ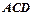 ;
;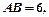
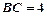 ,求
,求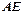 .
.

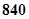 名职工,现采用系统抽样方法抽取
名职工,现采用系统抽样方法抽取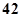 人做问卷调查,将
人做问卷调查,将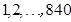 随机编号,则抽取的
随机编号,则抽取的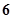 ,则抽取的编号落在区间
,则抽取的编号落在区间 的人数是 ;
的人数是 ;