题目内容
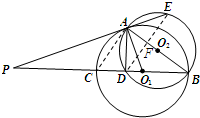
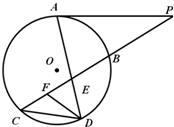
如图,⊙O1与⊙O2相交于A、B两点,AB是⊙O2的直径,过A点作⊙O1的切线交⊙O2于点E,并与BO1的延长线交于点P,PB分别与⊙O1、⊙O2交于C,D两点.
求证:
(1)PA•PD=PE•PC;
(2)AD=AE.

求证:
(1)PA•PD=PE•PC;
(2)AD=AE.

证明:(1)∵PE、PB分别是⊙O2的割线
∴PA•PE=PD•PB(2分)
又∵PA、PB分别是⊙O1的切线和割线
∴PA2=PC•PB(4分)
由以上条件得PA•PD=PE•PC(5分)
(2)连接AC、ED,设DE与AB相交于点F
∵BC是⊙O1的直径,∴∠CAB=90°
∴AC是⊙O2的切线.(6分)
由(1)知
=
,∴AC∥ED,∴AB⊥DE,∠CAD=∠ADE(8分)
又∵AC是⊙O2的切线,∴∠CAD=∠AED
又∠CAD=∠ADE,∴∠AED=∠ADE
∴AD=AE(10分)
∴PA•PE=PD•PB(2分)
又∵PA、PB分别是⊙O1的切线和割线
∴PA2=PC•PB(4分)
由以上条件得PA•PD=PE•PC(5分)
(2)连接AC、ED,设DE与AB相交于点F
∵BC是⊙O1的直径,∴∠CAB=90°
∴AC是⊙O2的切线.(6分)
由(1)知
| PA |
| PE |
| PC |
| PD |
又∵AC是⊙O2的切线,∴∠CAD=∠AED
又∠CAD=∠ADE,∴∠AED=∠ADE
∴AD=AE(10分)


练习册系列答案
相关题目
 点在圆
点在圆 直径
直径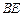 的延长线上,
的延长线上,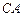 切圆
切圆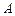 点,
点, 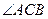 的平分线分别交
的平分线分别交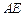 、
、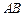 于点
于点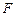 、
、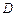 .
.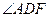 的度数;
的度数;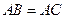 ,求
,求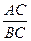 的值.
的值.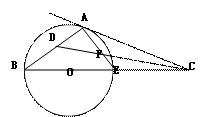
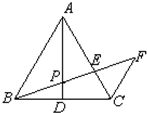


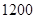 名学生对学校某项教改试验的意见,打算从中抽取一个容量为
名学生对学校某项教改试验的意见,打算从中抽取一个容量为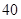 的样考虑用系统抽样,则分段的间隔
的样考虑用系统抽样,则分段的间隔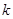 为_______________.
为_______________.