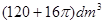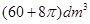题目内容
在一个锥体中，作平行于底面的截面，若这个截面面积与底面面积之比为1∶3，则锥体被截面所分成的两部分的体积之比为（ ）
A．1∶ | B．1∶9 | C．1∶ | D．1∶ |
D
解析试题分析：几何体中，体积比是相似比的立方，面积比是相似比的平方，直接求解即可．设小锥体的高为h1，大锥体的高为h2，利用一个锥体被平行于底面的截面所截得的小锥体与原锥体体积之比等于相似比的立方，
而这个截面面积与底面面积之比等于相似比的平方，即
，则借助于合分比性质可知锥体被截面所分成的两部分的体积之比为1∶，选D.
考点：几何体体积比与相似边比值的关系运用
点评：本题是基础题，考查几何体的体积比与相似比的关系，常用此法简化解题过程，同学注意掌握应用．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
某三棱锥的三视图如图所示，该三梭锥的表面积是（ ）
A．60+12 | B．56+ 12 |
| C．30+6 | D．28+6 |
在正方体
中，
是棱
的中点，
是侧面
内的动点，且
平面
，则
与平面所成角的正切值构成的集合是（ ）
A． | B． | C． | D． |
一个几何体的底面是正三角形，侧棱垂直于底面，它的三视图及其尺寸如下（单位cm），则该几何体的表面积为（ ）。
A．4(9+2 ) cm2 | B． cm2 | C． cm2 | D． cm |
一个空间几何体的三视图如图所示，则该几何体的表面积为（ ）
A． | B． | C． | D． |
的正方体，其三视图如图所示，则容器的容积为（ ）
如图是一个几何体的正视图和侧视图。其俯视图是面积为
的矩形。则该几何体的体积是
| A．8 | B． |
| C．16 | D． |