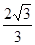题目内容
若三棱锥S-ABC的底面是以AB为斜边的等腰直角三角形,AB=2,SA=SB=SC=2,则该三棱锥的外接球的表面积为( )
A. | B. | C. | D. |
D
解析试题分析:说明P在底面上的射影是AB的中点,也是底面外接圆的圆心,求出球的半径,即可求出外接球的表面积.由题意,点P在底面上的射影D是AB的中点,是三角形ABC的外心,令球心为O,如图在直角三角形ODC中,由于
球的表面积为 ,故选D.
,故选D.
考点:球的表面积
点评:本题是基础题,考查球的内接体,球的表面积,考查计算能力,空间想象能力,转化思想的应用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
某几何体的三视图如图所示,当 取最大值时,这个几何体的体积为( )
取最大值时,这个几何体的体积为( )
A. | B. | C.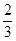 | D.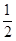 |
在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为( )
A.1∶ | B.1∶9 | C.1∶ | D.1∶ |
一个空间几何体的三视图如右图所示,其中主视图和侧视图都是半径为 的圆,且这个几何体是球体的一部分,则这个几何体的表面积为( ).
的圆,且这个几何体是球体的一部分,则这个几何体的表面积为( ).
| A.3π | B.4π | C.6π | D.8π |
若一个螺栓的底面是正六边形,它的主视图和俯视图如图所示,则它的体积是
A.27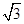 +12π +12π | B.9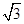 +12 +12 |
C.27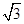 +3π +3π | D. 54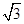 +3π +3π |
在空间,下列命题正确的是( )
| A.平行直线的平行投影重合 | B.平行于同一直线的两个平面平行 |
| C.垂直于同一平面的两个平面平行 | D.垂直于同一平面的两条直线平行 |
已知一个棱长为 的正方体的顶点都在球面上,则球的表面积等于( )
的正方体的顶点都在球面上,则球的表面积等于( )
A. | B. |
C. | D. |
 的各顶点都在一个半径为
的各顶点都在一个半径为 的球面上,球心
的球面上,球心 在
在 上,
上, 底面
底面 ,
,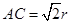 ,则球的体积与三棱锥体积之比是( )
,则球的体积与三棱锥体积之比是( )


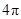
 ,BC=1,E为线段DC上一动点,现将
,BC=1,E为线段DC上一动点,现将 AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为
AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为