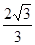题目内容
在正方体 中,
中, 是棱
是棱 的中点,
的中点, 是侧面
是侧面 内的动点,且
内的动点,且 平面
平面 ,则
,则 与平面
与平面 所成角的正切值构成的集合是( )
所成角的正切值构成的集合是( )
A. | B. | C. | D. |
D
解析试题分析:因为 是棱
是棱 的中点,设G,I分别为BC、C1B1边上的中点,则ABEG四点共面,且平面A1BGE∥平面B1EI,
的中点,设G,I分别为BC、C1B1边上的中点,则ABEG四点共面,且平面A1BGE∥平面B1EI,
又∵A1F∥面D1AE,∴F落在线段EI上,
设EI的中点为J,则当F与J重合时,A1F与平面 所成角的正切值有最大值2
所成角的正切值有最大值2 ,
,
当F与E或I重合时,A1F与平面 所成角的正切值有最小值2,
所成角的正切值有最小值2,
故 与平面
与平面 所成角的正切值构成的集合是{t|2≤t≤2
所成角的正切值构成的集合是{t|2≤t≤2 }
}
故选D.
考点:本题主要考查正方体的几何特征,直线与平面所成的角。
点评:中档题,首先明确“F落在线段HI上”是解题的关键,确定角的正切值,主要是在直角三角形中。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个几何体的三视图如右图所示,且其左视图是一个等边三角形,则这个几何体的体积为( )
A. | B. |
C. | D.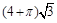 |
平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为 ,则此球的体积为
,则此球的体积为
A. π π | B.4 π π | C.4 π π | D.6 π π |
如果一个几何体的三视图如图所示,则该几何体的表面积为( )
A.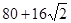 | B. | C.96 | D.80 |
某几何体的三视图如图所示,当 取最大值时,这个几何体的体积为( )
取最大值时,这个几何体的体积为( )
A. | B. | C.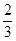 | D.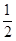 |
在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为( )
A.1∶ | B.1∶9 | C.1∶ | D.1∶ |




 的各顶点都在一个半径为
的各顶点都在一个半径为 的球面上,球心
的球面上,球心 在
在 上,
上, 底面
底面 ,
,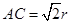 ,则球的体积与三棱锥体积之比是( )
,则球的体积与三棱锥体积之比是( )


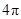
 ,BC=1,E为线段DC上一动点,现将
,BC=1,E为线段DC上一动点,现将 AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为
AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为