题目内容
(本题满分12分)已知椭圆 ,过中心O作互相垂直的线段OA、OB与椭圆交于A、B, 求:
,过中心O作互相垂直的线段OA、OB与椭圆交于A、B, 求:
(1) 的值
的值
(2)判定直线AB与圆 的位置关系
的位置关系
(文科)(3)求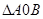 面积的最小值
面积的最小值
(理科)(3)求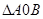 面积的最大值
面积的最大值
 ,过中心O作互相垂直的线段OA、OB与椭圆交于A、B, 求:
,过中心O作互相垂直的线段OA、OB与椭圆交于A、B, 求:(1)
 的值
的值(2)判定直线AB与圆
 的位置关系
的位置关系(文科)(3)求
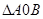 面积的最小值
面积的最小值(理科)(3)求
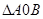 面积的最大值
面积的最大值(1) (2)相交(文科)(3)
(2)相交(文科)(3) (理科)(3)
(理科)(3)
 (2)相交(文科)(3)
(2)相交(文科)(3) (理科)(3)
(理科)(3)
(1)设线段OA所在的直线方程为 ,则线段OB所在的直线方程为
,则线段OB所在的直线方程为 ,分别与椭圆方程联立得A、B两点的坐标,代入两点间距离公式可证出结论;(2)根据(1)中A、B两点的坐标写出直线AB的方程,要考虑斜率是否存在,求出原点到直线AB的距离与2比较可得结论;
,分别与椭圆方程联立得A、B两点的坐标,代入两点间距离公式可证出结论;(2)根据(1)中A、B两点的坐标写出直线AB的方程,要考虑斜率是否存在,求出原点到直线AB的距离与2比较可得结论;
(3)由(2)得原点到直线AB的距离,再求出A、B两点间的距离,用 表示
表示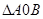 面积,构造函数求出最值。
面积,构造函数求出最值。
 ,则线段OB所在的直线方程为
,则线段OB所在的直线方程为 ,分别与椭圆方程联立得A、B两点的坐标,代入两点间距离公式可证出结论;(2)根据(1)中A、B两点的坐标写出直线AB的方程,要考虑斜率是否存在,求出原点到直线AB的距离与2比较可得结论;
,分别与椭圆方程联立得A、B两点的坐标,代入两点间距离公式可证出结论;(2)根据(1)中A、B两点的坐标写出直线AB的方程,要考虑斜率是否存在,求出原点到直线AB的距离与2比较可得结论;(3)由(2)得原点到直线AB的距离,再求出A、B两点间的距离,用
 表示
表示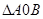 面积,构造函数求出最值。
面积,构造函数求出最值。
练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
 :
: ,a,b为常数),动圆
,a,b为常数),动圆 ,
, 。点
。点 分别为
分别为 与
与 与直线
与直线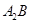 交点M的轨迹方程;
交点M的轨迹方程; 与
与 四点,其中
四点,其中 ,
, 。若矩形
。若矩形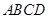 与矩形
与矩形 的面积相等,证明:
的面积相等,证明: 为定值。
为定值。

 的离心率为
的离心率为 ,两焦点之间的距离为4.
,两焦点之间的距离为4.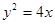 于A、B两点,
于A、B两点, 分别为椭圆
分别为椭圆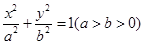 的左、右顶点,若在椭圆上存在异于
的左、右顶点,若在椭圆上存在异于 ,使得
,使得 ,其中
,其中 为坐标原点,则椭圆的离心率
为坐标原点,则椭圆的离心率 的取值范围是
的取值范围是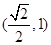


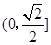
 的长轴两端点为
的长轴两端点为 ,若椭圆
,若椭圆 上存在点
上存在点 ,使得
,使得 ,求椭圆
,求椭圆 的取值范围____________;
的取值范围____________;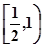



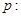 “椭圆
“椭圆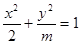 的焦点在
的焦点在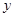 轴上”;
轴上”;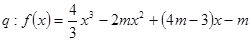 在
在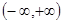 上单调递增,若“
上单调递增,若“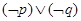 ”为假,求
”为假,求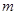 的取值范围.
的取值范围.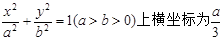 的点到左焦点的距离大于它到右准线的距离,则椭圆离心率e的取值范围是 .
的点到左焦点的距离大于它到右准线的距离,则椭圆离心率e的取值范围是 . 的焦点为
的焦点为 ,点p在椭圆上,若
,点p在椭圆上,若 ,则
,则
 的大小为
的大小为  的曲线恰好有两个不同的公共点,则实数
的曲线恰好有两个不同的公共点,则实数 的取值范围是
的取值范围是

