题目内容
已知椭圆
 的离心率为
的离心率为 ,两焦点之间的距离为4.
,两焦点之间的距离为4.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过椭圆的右顶点作直线交抛物线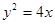 于A、B两点,
于A、B两点,
(1)求证:OA⊥OB;
(2)设OA、OB分别与椭圆相交于点D、E,过原点O作直线DE的垂线OM,垂足为M,证明|OM|为定值.

 的离心率为
的离心率为 ,两焦点之间的距离为4.
,两焦点之间的距离为4.(Ⅰ)求椭圆的标准方程;
(Ⅱ)过椭圆的右顶点作直线交抛物线
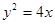 于A、B两点,
于A、B两点,(1)求证:OA⊥OB;
(2)设OA、OB分别与椭圆相交于点D、E,过原点O作直线DE的垂线OM,垂足为M,证明|OM|为定值.
(Ⅰ) (Ⅱ)见解析
(Ⅱ)见解析
 (Ⅱ)见解析
(Ⅱ)见解析(1)由2c=4,c/a=1/2,可求出a,进而求出b,问题解决.
(II)(1)若直线的斜率存在,可设直线方程为
然后与抛物线方程联立,消去y转化为 ,
,
借助韦达定理证明 即可.
即可.
斜率不存在的情况要单独考虑.
(2) 设 、
、 ,直线
,直线 的方程为
的方程为 ,代入
,代入 ,得
,得 .于是
.于是 .
.
 ,
, .可得
.可得 .
.
再证明原点到直线 的距离
的距离 为定值
为定值
解:(Ⅰ)由 得
得 ,故
,故 . ………………………3分
. ………………………3分
所以,所求椭圆的标准方程为 ……………………………4分
……………………………4分
(Ⅱ)(1)若直线的斜率存在,可设直线方程为 ……………5分
……………5分
代入抛物线方程整理得
设点A( )点B(
)点B( ),则
),则 ,
, ………7分
………7分

所以 ……………………………………………9分
……………………………………………9分
若直线斜率不存在,则A(4,4)B(4,-4),同样可得 …………10分
…………10分
(2)设 、
、 ,直线
,直线 的方程为
的方程为 ,代入
,代入 ,得
,得 .于是
.于是 .从而
.从而
 ,
, .得
.得 .∴原点到直线
.∴原点到直线 的距离
的距离 为定值…15分
为定值…15分
(II)(1)若直线的斜率存在,可设直线方程为

然后与抛物线方程联立,消去y转化为
 ,
,借助韦达定理证明
 即可.
即可.斜率不存在的情况要单独考虑.
(2) 设
 、
、 ,直线
,直线 的方程为
的方程为 ,代入
,代入 ,得
,得 .于是
.于是 .
. ,
, .可得
.可得 .
.再证明原点到直线
 的距离
的距离 为定值
为定值解:(Ⅰ)由
 得
得 ,故
,故 . ………………………3分
. ………………………3分所以,所求椭圆的标准方程为
 ……………………………4分
……………………………4分(Ⅱ)(1)若直线的斜率存在,可设直线方程为
 ……………5分
……………5分代入抛物线方程整理得

设点A(
 )点B(
)点B( ),则
),则 ,
, ………7分
………7分
所以
 ……………………………………………9分
……………………………………………9分若直线斜率不存在,则A(4,4)B(4,-4),同样可得
 …………10分
…………10分(2)设
 、
、 ,直线
,直线 的方程为
的方程为 ,代入
,代入 ,得
,得 .于是
.于是 .从而
.从而
 ,
, .得
.得 .∴原点到直线
.∴原点到直线 的距离
的距离 为定值…15分
为定值…15分
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 :
: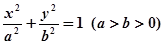 的中心
的中心 为圆心,
为圆心, 为半径的圆称为该椭圆的“准圆”.设椭圆
为半径的圆称为该椭圆的“准圆”.设椭圆 ,左焦点为
,左焦点为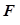 ,上顶点为
,上顶点为 ,且满足
,且满足 ,
,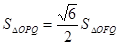 .
. 及其“准圆”的方程;
及其“准圆”的方程; (不与坐标轴垂直)与椭圆
(不与坐标轴垂直)与椭圆 、
、 两点,试证明:当
两点,试证明:当 时,试问弦
时,试问弦 轴上的双曲线的离心率
轴上的双曲线的离心率 ,其焦点到渐近线的距离为1,则此双曲线的方程为( )
,其焦点到渐近线的距离为1,则此双曲线的方程为( )



 的离心率为( )
的离心率为( )

 为椭圆
为椭圆 的两个焦点,P为椭圆上一点且
的两个焦点,P为椭圆上一点且 ,则此椭圆离心率的取值范围是( )
,则此椭圆离心率的取值范围是( )



 ,过中心O作互相垂直的线段OA、OB与椭圆交于A、B, 求:
,过中心O作互相垂直的线段OA、OB与椭圆交于A、B, 求: 的值
的值 的位置关系
的位置关系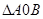 面积的最小值
面积的最小值 的右焦点为
的右焦点为 ,点
,点 在圆
在圆 上任意一点(点
上任意一点(点 的切线交椭圆
的切线交椭圆 于两点
于两点 、
、 .
. ;
;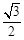 ,求线段
,求线段 长度的最大值.
长度的最大值.
 、
、 ,
, 是直线
是直线 上任意一点,以A、B为焦点的椭圆过点P.记椭圆离心率
上任意一点,以A、B为焦点的椭圆过点P.记椭圆离心率 关于
关于 的函数为
的函数为 ,那么下列结论正确的是 ( )
,那么下列结论正确的是 ( ) 的焦距为
的焦距为 ,则实数
,则实数 .
.